定常媒体での質量拡散移動

質量拡散移動の支配方程式は以下の様になります[34]。

$\displaystyle \boldsymbol{ j}_A = - \rho \boldsymbol{D}_{AB}\nabla m_A$

(227)

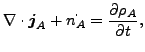$\displaystyle \nabla \cdot \boldsymbol{ j}_A + \dot{n_A} = \frac{\partial \rho_A}{\partial t},$

(228)

ここで

$\displaystyle m_A = \frac{\rho_A}{\rho_A + \rho_B}$

(229)

$\displaystyle \rho = \rho_A + \rho_B.$

(230)

です。上記方程式で j_A は種 A の質量フラックス、D_AB は質量拡散率、m_A は種 A の質量分率、ρ_A は種 A の密度です。また $\dot{n_A}$ は混合物単位体積あたりの種 A の質量増加率です。これらは以下の様な式として書くこともできます。

$\displaystyle \boldsymbol{ J}_A^* = - C \boldsymbol{D}_{AB}\nabla x_A$

(231)

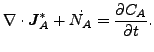$\displaystyle \nabla \cdot \boldsymbol{ J}_A^* + \dot{N_A} = \frac{\partial C_A}{\partial t}.$

(232)

ここで

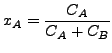$\displaystyle x_A = \frac{C_A}{C_A + C_B}$

(233)

C = C_A + C_B

(234)

です。ここで J^*_A は種 A のモル・フラックス、D_AB は質量拡散率、x_A は種 A のモル分率、C_A は種 A のモル濃度です。また $\dot{N_A}$ は種 A のモル濃度増加率です。

これらから以下のような結果が得られます。

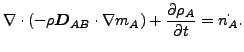$\displaystyle \nabla \cdot (- \rho \boldsymbol{ D}_{AB} \cdot \nabla m_A)+ \frac{\partial \rho_A}{\partial t} = \dot{n_A} .$

(235)

または

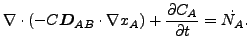$\displaystyle \nabla \cdot (- C \boldsymbol{ D}_{AB} \cdot \nabla x_A)+ \frac{\partial C_A}{\partial t} = \dot{N_A} .$

(236)

C と ρ が定数の場合にはこれらは以下の様に変形できます。

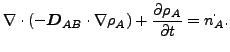$\displaystyle \nabla \cdot (- \boldsymbol{ D}_{AB} \cdot \nabla \rho_A)+ \frac{\partial \rho_A}{\partial t} = \dot{n_A} .$

(237)

または

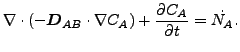$\displaystyle \nabla \cdot (- \boldsymbol{ D}_{AB} \cdot \nabla C_A)+ \frac{\partial C_A}{\partial t} = \dot{N_A} .$

(238)

熱方程式と比較すると、その対応関係は表（16）の様になります。

guido dhondt 2016-03-08