浅水方程式による流れ
ケース
$FOAM_TUTORIALS/incompressible/shallowWaterFoam/squareBump
概要
深さ方向の流速分布を無視できる系で、浅水方程式を使用して流れ計算を行います。解かれる浅水方程式は以下の通りです。
ここで h、u の各変数はそれぞれ流体の深さ(液面高さ)、流速ベクトルです。また f はコリオリ力、g は重力加速度、h0 は平均流体の深さからのずれ、τω、τb はそれぞれ液体表面、液体底面からの応力です。
流体が領域 inlet(赤色部)から流速 (0.1, 0, 0) m/s に流入し、領域 outlet(緑色部)から流出します。流路壁面(青色部)は すべり壁とし、Z方向は1メッシュとして2次元問題として計算を行います。また流路中央部のみ流体の深さを 0.009 m とし他は 0.01 mとします。
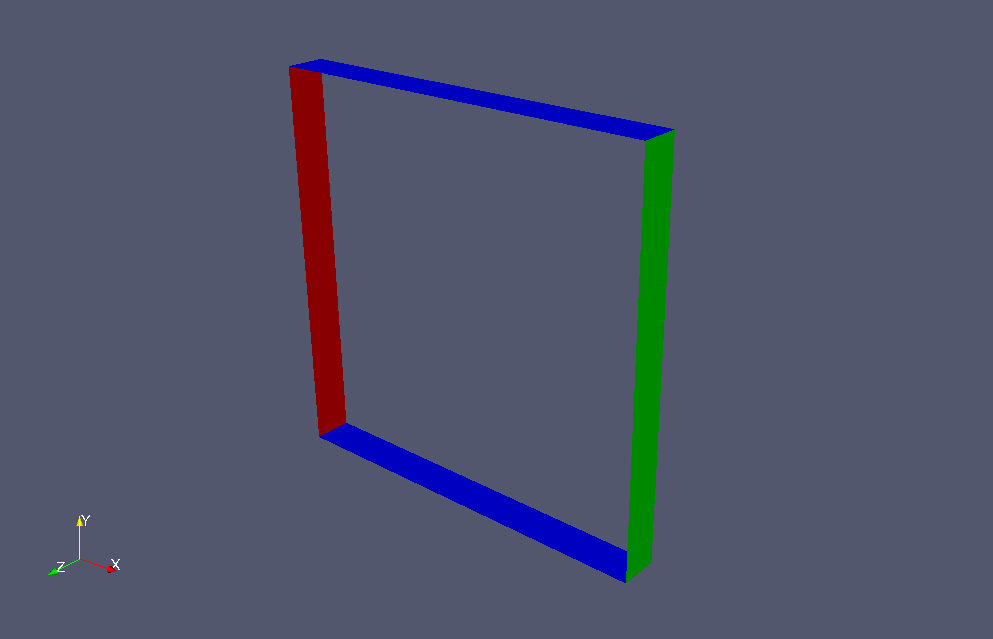 モデル形状
モデル形状
 流体の深さの定義
流体の深さの定義
メッシュは以下の通りです。
 メッシュ
メッシュ
流体の深さを可視化するために ParaView 上で「Properties」タブの「h」にチェックを入れます。
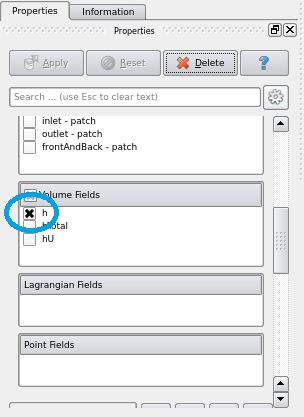 「h」にチェック
「h」にチェック
計算結果は以下の通りです。
流体の深さ分布(h)
 0秒での流体の深さ分布(h)
0秒での流体の深さ分布(h)
 1秒での流体の深さ分布(h)
1秒での流体の深さ分布(h)
 100秒での流体の深さ分布(h)
100秒での流体の深さ分布(h)
中央の突起部で波が発生したのち、定常状態に近づいていく様子がわかります。
実行コマンド
cp -r $FOAM_TUTORIALS/incompressible/shallowWaterFoam/squareBump squareBump
cd squareBump
blockMesh
shallowWaterFoam
paraFoam
cd squareBump
blockMesh
shallowWaterFoam
paraFoam
計算時間
4.87秒 ※シングル、Inter(R) Core(TM) i7-2600 CPU @ 3.40GHz 3.40GHz

