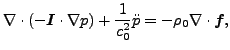音響

気体での線形音響計算は熱伝達計算に非常によく似ています。一様な基準圧力 p₀ と基準密度 ρ₀（そしてその結果として気体法則から求まる一様温度 T₀）を使うと空間内の圧力変化は以下の様になります。

$\displaystyle \nabla \cdot (- \boldsymbol{I} \cdot \nabla{p}) + \frac{1}{c_0^2} \ddot{p} = - \rho_0 \nabla \cdot \boldsymbol{f},$

(203)

ここで I は2次精度の単位テンソル（簡略化されている場合は単位行列）、c₀ は以下を満たす音速です。

γ は低圧での比熱を定積での比熱で割った比（空気の場合 γ = 1.4）、R は固有気体定数（空気の場合 R = 287 J/(kgK)）、T₀ は絶対基準温度（K）です。さらに運動量バランスは以下の様に書き下せます。

詳細については[20]、[2]を参照してください。式（203）はよく知られた波動方程式にです。熱方程式と比較すると、その対応関係は表（9）の様になります。

**表 9:**熱方程式と気体運動量方程式の間の対応関係
熱の諸量	気体の諸量
T	p
q	$\rho_0 (\boldsymbol{ a} - \boldsymbol{ f})$
q_n	$\rho_0 (a_n - f_n)$
κ	I
ρh	$- \rho_0 \nabla \cdot \boldsymbol{ f}$
ρc	$\frac{ 1}{c_0^2}$

ただし時間微分は熱方程式では1次、気体運動量方程式では2次であることに注意してください。つまり CalculiX では非定常な熱移動の機能は気体方程式に対して使うことができないのです。とはいえ周波数オプションは使えますし、結果固有モードは以降のモード動解析・定常状態動解析で使用できます。また固体の支配方程式は2次の時間微分であることを思い出してください（[18]）。

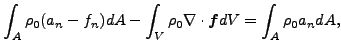$\displaystyle \int_ A \rho_0 (a_n -f_n) d A - \int_ V \rho_0 \nabla \cdot \boldsymbol{ f} dV = \int_A \rho_0 a_n dA,$

(206)

これは境界での法線熱フラックスが基準密度に加速度をかけたものと同等であることを意味しています。つまり境界では圧力または加速度のどちらかがわかっていなければならないのです。