は電荷密度、ε0 は自由空間の誘電率(ε0= 8.8542×10-12 C2/Nm2)です。電場 E は単位電荷での力です。
金属ではこれは電気伝導度 σc による電流密度 j と関係します[5]。
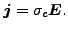 |
(213) |
自由空間では電場は伝導表面に対して局所的に垂直になります。表面近くでは電場の大きさは表面電気密度 σ に比例します[22]。
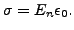 |
(214) |
式(211)を式(212)に代入すると以下の支配方程式が求まります。
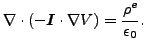 |
(215) |
熱方程式と比較すると、その対応関係は表(13)の様になります。静電気方程式は定常状態方程式で、熱容量に相当する項を持たないことに注意してください。
表 13:熱方程式と(金属と自由空間の)静電気方程式の間の対応関係
| 熱の諸量 |
静電気の諸量 |
|---|
| T |
V |
| q |
E |
| qn |
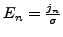 |
| κ |
I |
| ρh |
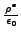 |
| ρc |
- |
静電気を扱う問題のひとつは亀裂伝搬による電位低下です。事前に定義した電流が伝導試料に流されますが、亀裂伝搬によって試料区間は減少し、電気抵抗は増加します。これによって試料前後の電位が増加します。試料の有限要素計算( ρe=0 の静電気方程式)は電位と亀裂寸法の間の関係として定式化できます。この校正曲線は実験で各電位に対応する実際の亀裂寸法を求めることで決定できます。
もうひとつはコンデンサーの静電容量計算です。コンデンサー内の空間には空気が満たされているとし、(コンデンサーは蓄電されていないとして) ρe=0 の静電気方程式を適用します。コンデンサーのそれぞれの電極の電位を(例えばゼロと1に)固定すると電場は熱のアナロジーで計算可能です。式(214)によってこの電場は表面電荷密度を生み出します。この表面電荷密度を積分することで総電荷量が求まります。この総電荷量を(ここまでで述べた式のひとつである)電位差で割ることで静電容量が定義されます。
誘電問題では式(212)が以下の様に変更されます。
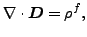 |
(216) |
ここで D は電気変位、ρf は自由電荷密度[22]です。電気変位は以下の式によって電場と結びついています。
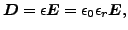 |
(217) |
ここで ε は誘電率、εr は比誘電率(通常 εr>1。例えばシリコンでは εr=11.68)です。この時、支配方程式は以下の様になります。
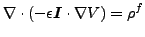 |
(218) |
さらに表(14)のようなアナロジーが考えられます。式(214)は以下の様に変形できます。
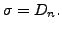 |
(219) |
表 14:熱方程式と(非誘電材料の)静電気方程式の間の対応関係
| 熱の諸量 | 静電気の諸量 |
|---|
| T | V |
| q | D |
| qn | Dn |
| κ | εI |
| ρh | ρf |
| ρc | - |
導電体の総電荷に相当する熱の量は総熱流量です。異方性材料では ε は2次精度のテンソルになることに注意してください。
次へ
上へ
前へ
目次へ
次へ:Stationary groundwater flow
上へ:Types of analysis
前へ:Irrotational incompressible inviscid flow
目次へ
guido dhondt
2016-03-08
![]()
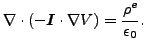
![]()
![]()
![]()
![]()