 |
このセクションは、*NODE PRINT カード、*NODE FILE カード、*NODE OUTPUT カードで RF を選択した際にユーザーが期待した通りの出力が得られないことがあるため用意されました。RF を使用すると節点にかかる全外力の合計が得られます。この外力は荷重と反作用力の合計と見なすことができます。いくつか例を見てみましょう。
図128はC3D20R要素ひとつだけでモデル化されたサイズ1 x 1 x 0.1の板の上面を表しています。表示されているのは要素の上面だけです。この面に属するすべての節点を荷重方向に固定したとしましょう。節点1には大きさ P の外部点荷重が適用されます。この節点は荷重方向に固定されているので大きさ R=P の反作用力が発生します。合計の力の大きさ、つまり点荷重と反作用力を足した値はゼロです。これがこの節点のために RF を選択した場合にユーザーが取得する値です。
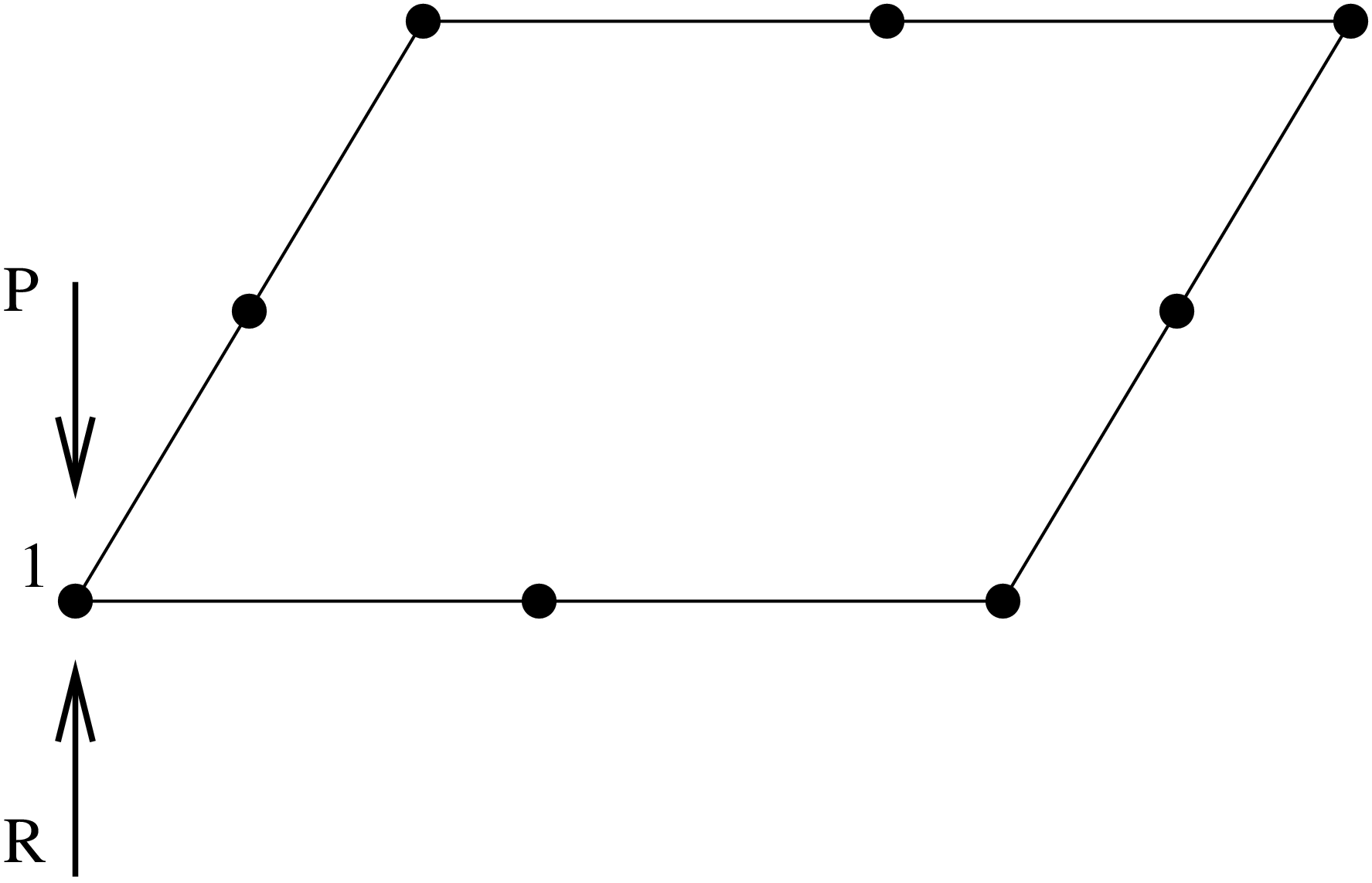
図129は同じ板ですが、今回は上面には大きさ1の圧力がかかっています。この板もC3D20R要素ひとつで作成されていて、かかっている圧力と等価な等価な点荷重は図に示す通りです。板の境界上にある節点(今回の例では全ての節点が境界上にあるので、これは全ての節点を意味します)は全て荷重方向に固定されているとしましょう。この時、各節点には荷重と等しい反作用力が生じます。再び各節点での合力はゼロになり、これが*NODE PRINT カード、*NODE FILE カード、*NODE OUTPUT カードでユーザーが得る力になります。
さて次は板を4つの2次要素でメッシュ化します。図130がその様子です。板の境界は全て固定されています。節点につけられた番号は大きさ1の均一な圧力と対応する節点力です。境界節点での外力の合計を知りたいとしましょう(例えば *NODE PRINT カードで RF を選択し、パラメーター TOTALS=ONLY を設定)。外力は反作用力と荷重の合計になり、反作用力の合計は-1です。境界節点での荷重は図130の丸がついていないもので、合計すると 5/12 です。この結果、境界節点でに外力の合計は -7/12 になります。
さらに細かいメッシュを使用すると、境界節点での外力の合計値は-1に近づいていきます。
簡単に言えば RF の選択によって得られるのは反作用力ろ荷重の合計であるということです。選択節点を持つ要素に働く荷重が *DLOAD カードによって設定されたものではなく、節点事態に *CLOAD カードで荷重が設定されていない場合にのみ、これは反作用力と等しくなります。