 |
この演習の目的は鉄筋コンクリート製の片持ち梁の自重による応力を計算することです。この種の問題で注意しなければならないのは複合材料としての構造体の取り扱いと圧縮のみ材質(コンクリート)の存在です。
入力デッキは次のようなります。
*NODE, NSET=Nall
1,1.000000000000e+01,0.000000000000e+00,0.000000000000e+00
...
*ELEMENT, TYPE=S8R, ELSET=Eall
1, 1, 2, 3, 4, 5, 6, 7, 8
2, 2, 9, 10, 3, 11, 12, 13, 6
...
** 左側を命名
*NSET,NSET=Nleft
49,
50,
52,
** 右側を命名
*NSET,NSET=Nright
1,
4,
8,
*MATERIAL,NAME=COMPRESSION_ONLY
*USER MATERIAL,CONSTANTS=2
1.4e10, 1.e5
*DENSITY
2350.
*MATERIAL,NAME=STEEL
*ELASTIC
210000.e6,.3
*DENSITY
7800.
*SHELL SECTION,ELSET=Eall,COMPOSITE
.09,,COMPRESSION_ONLY
.01,,STEEL
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
.1,,COMPRESSION_ONLY
*BOUNDARY
Nleft,1,6
*STEP,NLGEOM
*STATIC
1.,1.
*DLOAD
Eall,GRAV,9.81,0.,0.,-1.
*NODE FILE
U
*EL FILE
S
*END STEP
梁は断面1x1m2、長さ10mです。 コンクリートの密度は2350kg / m3で、鉄の密度は7800kg / m3です。 またヤング率はそれぞれ14000MPa、210000MPaです。 鉄材は上面から9.5cmの位置の梁上部のみに設定され、その厚みは1cmです (実際には鉄材は複数の棒としてコンクリート内に配置されます。薄い層状のモデル化は近似です。複数の棒の全体断面は層状断面と同じであることに注目してください)。 シェル構造に対して複合材機能を使用することで入力は大幅に簡略化されます。この機能は(今はまだ)ビーム要素では利用できないことに注意してください。 結果、梁は幅1m、長さ10mの平板としてモデル化されます。*SHELL SECTION カードのすぐ下に、梁の上から順に層の厚さとその材質がリストアップされています。 この方向(上から下)はシェル要素の法線方向によって制御されます(法線方向は *ELEMENT カード下の要素節点の並び順によって制御されます)。 複合シェルでは各層の断面には2つの積分点が存在します。ここでは必ずS8R要素を使用しなければなりません。 中立軸の位置を把握するために複数の層を使って断面のコンクリート部分をモデル化します(コンクリートは全て合わせて10層、鉄は1層)。
コンクリートは引っ張りには耐えられませんが、一方で 圧縮に対しては大きな線形弾性を持ちます。 これはCOMPRESSION_ONLY物性モデルでモデル化可能です。 これはCalculiXではユーザー物性の例のひとつです。ユーザー物性の名前は決められた文字列で始まり、今回の場合は"COMPRESSION_ONLY"がそれです。 残りの64文字(物性名は最長で80文字です)は自由に選ぶことができますが、今回の入力デッキでは追加文字は設定されていません。 ただし圧縮のみ物性が複数ある場合には(区別のために)必ず追加文字を設定する必要があります。 "COMPRESSION_ONLY"物性は2つの定数で特徴づけられます。 ひとつ目はヤング率、2つ目はユーザーが許容する最大引張応力で今回の場合は0.1 MPaです(SI単位系が使用されています)。
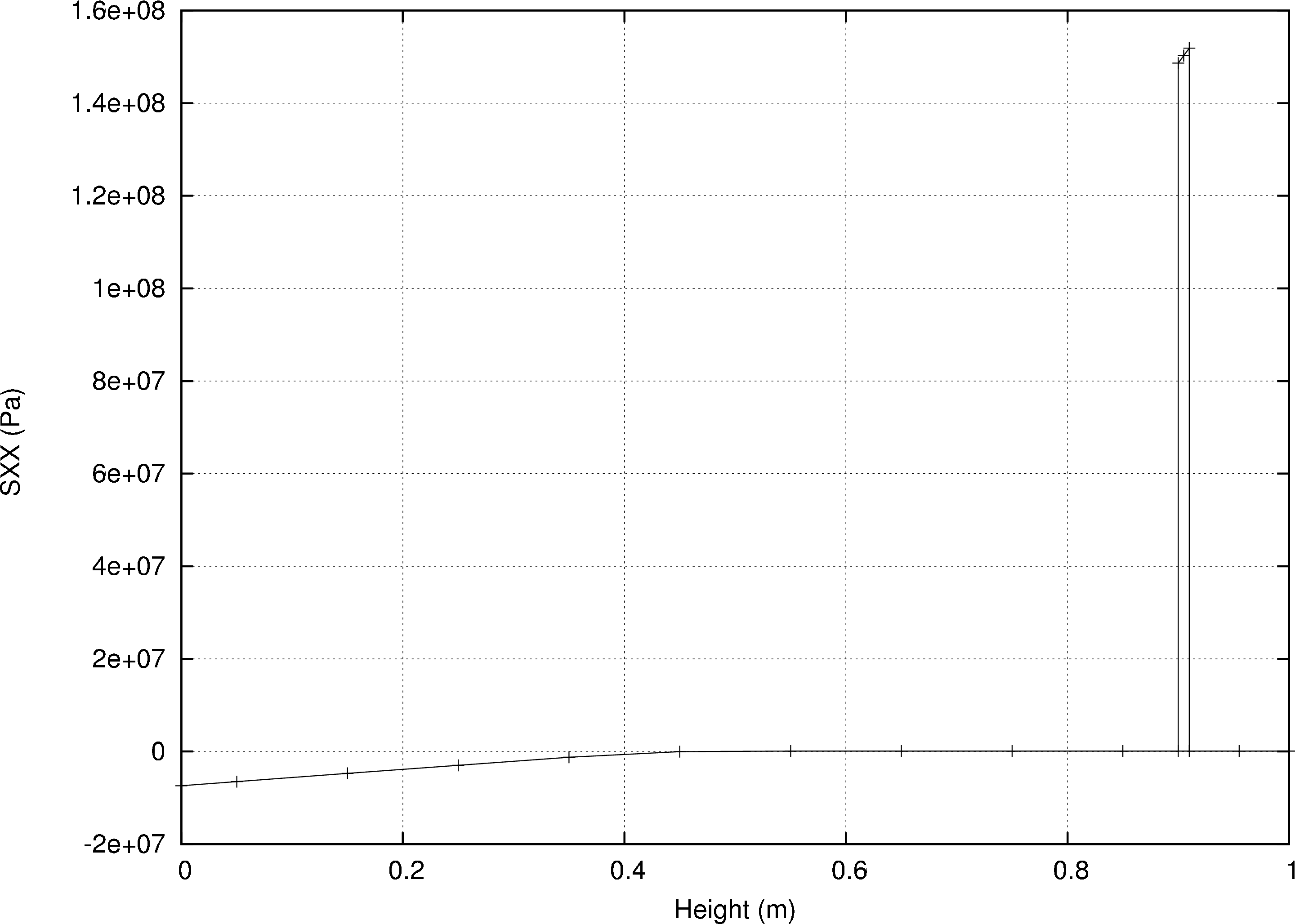
単純な梁理論([56])を使うと鉄材部分で引張応力が152.3MPaであること、コンクリート部の下縁で最大圧縮応力が7.77 MPaであることがわかります。 有限要素計算(図41)ではそれぞれ152MPa 、7.38 MPaと求まり、非常に近い値を得られます。 CalculiXでは複合構造のグラフィック出力は常に3次元に拡張されます。図42を見ると複合材の正しい寸法が表示されていること、薄い鉄の層で高い引張応力が出ていることがわかります。