座屈計算

座屈荷重を計算するためにはルーチン arpackbu.c が呼び出されます。座屈計算では以下の手順が必要になります。

• 座屈荷重による応力の計算。これは mafillsm.f での方程式系の準備、SPOOLES を使用した系の求解、results.f での応力の決定を意味します。
• 前の静的ステップの剛性行列 [K] から作成される座屈固有値系（代変形剛性と応力剛性を含む）と座屈荷重の応力剛性行列 [KG] の準備[18]
• 開始値 σ = 1 でのループ
  • [K - σKG] の LU 分解
  • ARPACK を使用した座屈係数の反復計算
  • 座屈モード の決定
  • 5σ < 座屈係数 < 50000σ の場合はループを終了、それ以外の場合は σ = 座屈係数 / 500 として繰り返し
• 応力とそれ以外のフィールドを決定

ARPACK（モード4、参照[41]）での座屈モードは以下の形の系を解くのに使用されます。

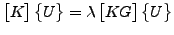(393)

ここで [K] は対称な正定値、[KG] は対称な非正定値です。固有値を見つけるための反復処理では以下を解かなければなりません。

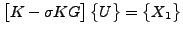(394)

また以下も計算しなければなりません。

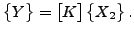(395)

周波数計算と同様、式（394）を解くための LU 分解（SPOOLES）は座屈係数を決定するループの前に行なわれます。式の左辺側は変化しないためです。式（395）での行列の乗算はルーチン op.f で扱われます。

周波数計算との大きな違いは座屈係数の値が正しいことを保証するために追加の反復ループが必要なことです。ここで σ の値は重要で、5σ < 座屈係数 < 50000σ が満たされていなければならないことが経験的に知られています。これが満たされていない場合には LU 分解から始まる処理全体が新しい値 σ = 座屈係数 / 500 で繰り返されます。必要な場合には最大で4回までこの反復が行なわれます。