周波数計算

周波数計算は、周期対称性の無い構造体ではサブルーチン arpack.c で、周期対称性の有る構造体では arpackcs.c で行なわれます。周波数計算は以下の手順を踏みます。

• mafillsm.f での剛性行列、質量行列の穴埋め。剛性行列は摂動パラメーターに依存して変わります。iperturb=1 ではもっとも新しい静的ステップでの応力剛性と大変形剛性が考慮されます（[18]）
• SPOOLES と ARPACK を使用して固有値系を解きます。
• .dat ファイルへのデータ保存を含め、results.f でフィールド変数を計算。
• out.f で結果を .frd 形式ファイルに保存。

固有値と固有モードはシフト逆転モードで解かれます。これは ARPACK のモード3に相当します（[41]）。以下の様な系を解きたいとしましょう。

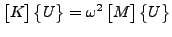(390)

この時、シフト逆転モードでは以下を解くアルゴリズムを要求します。

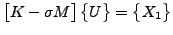(391)

また以下の計算も必要です。

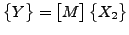(392)

ここで {X₁}、{X₂}は所与であり、σ はパラメーターです。CalculiX ではこれは1に設定されています。固有値と固有モードを決定するために反復処理中にこれらの演算が使用されます。最初の演算では SPOOLES が使用されます。SPOOLES じゃ LU 分解を用いて系を解きます。この分解は ARPACK によって始められる反復ループの前に行なわれます。これは式（391）の左辺側は常に同じであるためです。ループ内で行なわれるのは後退代入だけです。2番目の演算（式（392））はルーチン op.f で行なわれ、ごく簡単な行列操作です。このルーチンは行列の保存スキームに依存することに注意してください。

周期対称性の有る構造体では以下の追加処理を行う必要があります。

• 出力対象に複数セグメントが選択されている場合（*CYCLIC SYMMETRY MODEL キーワード・カードのパラメーター NGRAPH）は構造体を拡張。これは mafillsm 呼び出しの前に行なわれます。
• 基本セクターの結果に基づいて追加セクターの結果を計算。これはルーチン results.f 呼び出しの後で行なわれます。