次へ 上へ 前へ 目次へ
次へ：Seepage under a dam 上へ：Simple example problems 前へ：Frequency calculation of a 目次へ

加熱炉の熱計算

図16: 加熱炉の概略
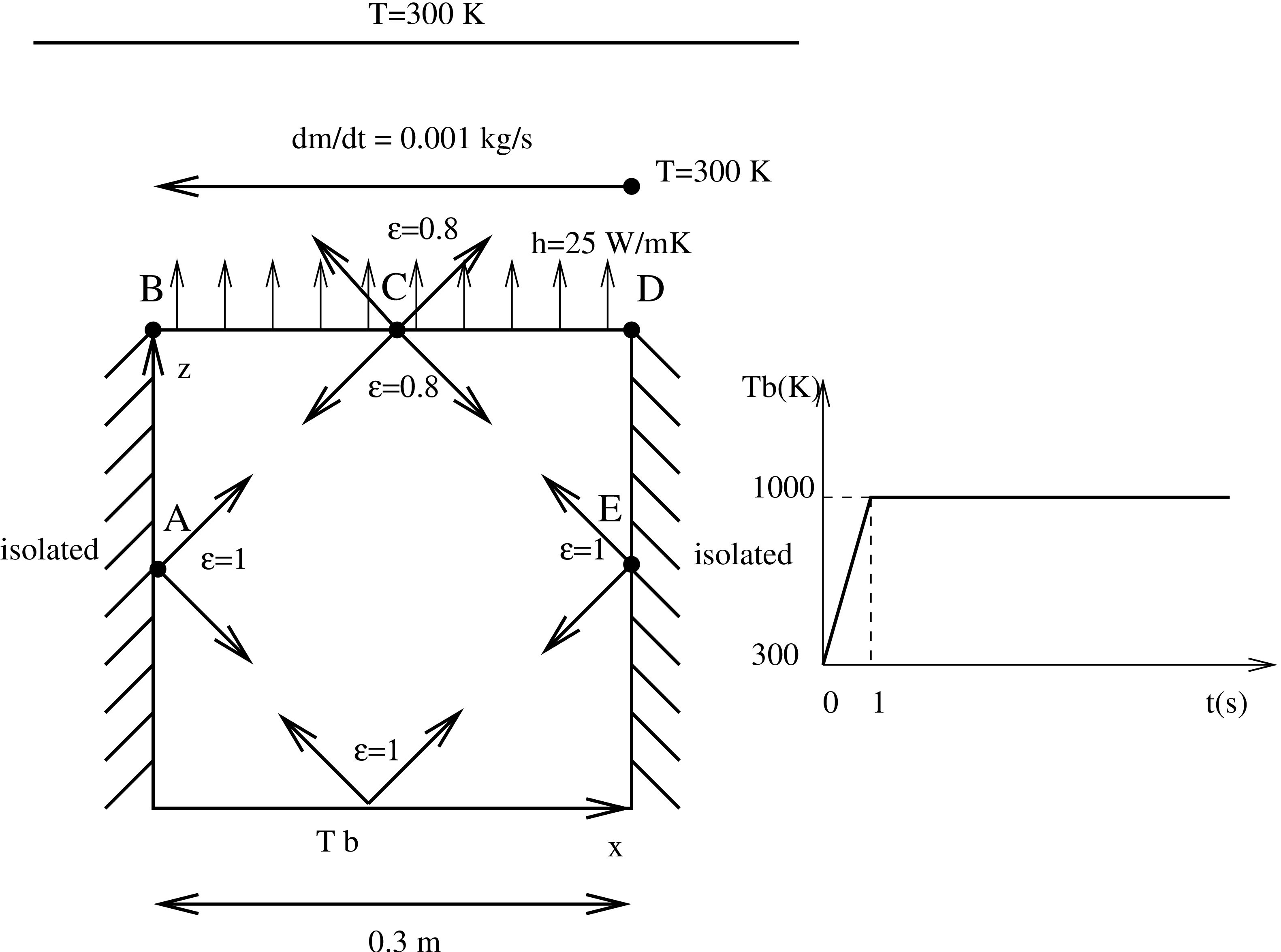
\begin{figure}\epsfig{file=furngeo.eps,width=11cm}\end{figure}

この問題では図16に図示されたような加熱炉の熱計算を行います。加熱炉は温度 Tb が与えられた底を持ちます。温度は非常に短い時間で300Kから1000Kまで線形に上昇し、その後、一定を保ちます。加熱炉の側壁は外部から隔絶されていますが、輻射によって加熱炉の他の壁と熱の交換が行われているものとします。側壁と底部の輻射率は ε=1 です。加熱炉の上部は輻射によって他の壁との熱交換をしているとし、雰囲気温度は300Kに固定されているとします。上部の輻射率は ε=0.8 です。さらに上部は 0.001 kg/s という一定の割合で流れる流体（空気）との対流によって熱交換を行っています。右上の隅における流体の温度は300Kです。炉の壁は10cmの鉄です。鉄の物質定数は、熱伝導率が κ=50W/mK、比熱が c=446W/kgK、密度が ρ=1kg/m3 です。 空気の比熱は cp=1000W/kgK、密度は ρ=1kg/m3です。対流係数は h=25W/m2K です。 加熱炉の寸法は 0.3×0.3×0.3m3（立方体）とします。t=0 では全ての部品が T=300Kであるとします。こここで位置A、B、C、D、Eでの温度が時間にともなってどのように変化するかを考えてみましょう。 

*NODE, NSET=Nall
       1,  3.00000e-01,  3.72529e-09,  3.72529e-09 
... 
603,-0.1,0.5,1.
...
613,0.8,0.5,1.
*ELEMENT, TYPE=S6, ELSET=furnace
     1,      1,      2,      3,      4,      5,      6
...
*ELEMENT,TYPE=D,ELSET=EGAS
301,603,609,604
...
305,607,613,608
*NSET,NSET=NGAS,GENERATE
603,608
*NSET,NSET=Ndown 
1, 
...
*PHYSICAL CONSTANTS,ABSOLUTE ZERO=0.,STEFAN BOLTZMANN=5.669E-8
*MATERIAL,NAME=STEEL
*DENSITY
7800.
*CONDUCTIVITY
50.
*SPECIFIC HEAT
446.
*SHELL SECTION,ELSET=furnace,MATERIAL=STEEL
0.01
*MATERIAL,NAME=GAS
*DENSITY
1.
*SPECIFIC HEAT
1000.
*FLUID SECTION,ELSET=EGAS,MATERIAL=GAS
*INITIAL CONDITIONS,TYPE=TEMPERATURE
Nall,300.
*AMPLITUDE,NAME=A1
0.,.3,1.,1.
*STEP,INC=100
*HEAT TRANSFER
0.1,1.
*BOUNDARY,AMPLITUDE=A1
Ndown,11,11,1000.
*BOUNDARY
603,11,11,300.
*BOUNDARY
609,1,1,0.001
...
*RADIATE
** Radiate based on down
1, R1CR,1000., 1.000000e+00
...
** Radiate based on top
51, R1CR, 1000.000000, 8.000000e-01
...
** Radiate based on side
101, R1CR, 1000.000000, 1.
...
** Radiate based on top
51, R2, 300.000000, 8.000000e-01
...
*FILM
51, F2FC, 604, 2.500000e+01
...
*NODE FILE
NT
*NODE PRINT,NSET=NGAS
NT
*END STEP
図17:加熱炉の入力デッキ

入力デッキは図17の様になります。入力デッキは節点の定義から始まります。 構造物で一番大きな節点番号は602で、節点603から節点608までは流体の節点です。 つまり流体中に追加で節点が定義されているのです（z=0.3が加熱炉の上部と対応し、z=0が底部と対応します）。 流体の節点603が流体温度が300Kの場所（"流入口"）に、節点608が"流出口"に対応します。 他の節点はその間に位置します。流体の節点の座標は実のところ計算には関係しません。 キーワード*FILMでの対流定義だけが加熱炉と流体の間の熱交換を支配します。 *ELEMENTカードでは6節点からなるシェル要素によって加熱炉の壁が定義されています。 さらに流体の節点も要素に割り当てられていて（要素タイプD）、これはネットワーク要素と呼ばれます。 これらの要素は流体に材質プロパティを割り当てるために必要になります。 そう、伝統的に材質プロパティは節点ではなく要素に割り当てられるのです。 各ネットワーク要素は温度が未知にの2つの末端節点と、要素を通過する質量流量を定義するのに使用される中間節点から構成されます。 603から613までの流体の節点は301から305までのネットワーク要素に割り当てられます。

次に2つの接点セットが定義されています。GASは全ての流体節点からなり、Ndownは加熱炉底部の全ての節点からなります。

輻射を考慮する解析では*PHYSICAL CONSTANTSカードが必要になります。 ケルビン温度で作業しているのでここでは絶対温度に0を定義し、またステファン・ボルツマン定数を定義しています。 この入力デッキでは一貫してSI単位を使用しています。

次に鉄の物質定数を定義します。熱解析では伝導率、比熱、密度を必ず定義する必要があります。 先の*ELEMENT文で定義した要素セットFURNACEに*SHELL SECTIONカードでSTEEL材料を割り当てます。 この要素セットには加熱炉を構成する全ての要素が含まれています。さらに厚さ0.01mが割り当てられています。

材料GASの物質定数は密度と比熱からなります。 これらは流体のため定数です。流体の熱伝導率は考えません。 材料GASは全てのネットワーク要素を含む要素セットEGASに割り当てられています。

*INITIAL CONDITIONSカードは全節点、つまり加熱炉の節点と流体の節点の初期温度300Kを定義しています。 *AMPLITUDEカードは(0.0, 0.3)から始まり、(1.0, 1.0)まで線形に増加するランプ関数を定義します。 この関数は加熱炉底部での温度の境界条件を定義するために使用されます。これでモデル定義は終わりです。

最初のステップにはt=0とt=1の間での温度境界条件の線形増加が記載されています。 *STEPカードの INC=100 パラメーターによってこのスッテプでは100進みます。 プロシージャは *HEAT TRANSFER です。つまり単純な熱解析、 未知数は温度だけで（変位など）力学的未知数は存在しない解析を行おうとしているということです。 タイムステップは1.0、初期の増分は0.1になっていて両方とも *HEAT TRANSFER カードの下の行に記載されています。 *HEAT TRANSFER カードにパラメーター STEADY STATE が無いのはこれが非定常解析であることを表しています。

次に来るのは温度境界条件で、加熱炉の底部を1000Kに固定し、ただし振幅A1で振動させます。 結果として温度境界条件は 0.3 x 1000 = 300K から開始し、線形に増加して t=1 s で 1000 K に到達します。 2番目の境界条件では（流体）節点603の温度を300Kに固定するよう指定します。これが流入温度です。 "11"が温度の自由度であることに注意してください。

流体の質量流量は *BOUNDARY カードで定義され、ネットワーク要素の中間節点の最初の自由度に適用されています。 最初の行は（流体）節点609の質量流量が0.001であることを意味しています。 節点609はネットワーク要素301の中間節点です。この流量は正の数なので流体は節点603から節点604に向かって、 つまりネットワーク要素301の1番目の節点から3番目の節点に向かって流れています。 ユーザーは質量保存則が保たれるように注意する必要があります（これは実際にはプログラムによってもチェックされます）。

輻射境界条件の最初のセットでは加熱炉の底部の上面が輻射率1の空洞輻射、1000Kの雰囲気温度で輻射するように指定しています。 空洞輻射では、どこかの形態係数が1に達しない場合に雰囲気温度が使用されます。1に足りない分は外部に向かって輻射しているのです。 各行の先頭の数字は要素で、ラベルの数字（各業の2番目の項目）は輻射にさらされる要素の面です。 一般的にはこれらの行はcgx（CalculiX GraphiX）によって自動的に生成されます。

図18: t=3001 sでの温度分布
\begin{figure}\epsfig{file=furntemp.ps,width=9cm}\end{figure}

図19:選択位置での温度

2番目、3番目のブロックは上部と側部のための加熱炉内部の空洞輻射を定義しています。 4番目のブロックは300Kに固定された外部に向かう加熱炉上面の輻射を定義しています。 上面の輻射率は0.8です。

次に来るのは薄膜条件です。対流係数 h=25W/mK によって加熱炉上面での強制対流が定義されています。 *FILM キーワードの下の最初の行は要素51の2番目の面が強制対流によって（流体）節点604と 相互作用していることを表しています。この行の最後の項目が対流係数です。 流体と相互作用する各面に関しては、それと相互作用する適切な流体節点を指定しなければなりません。

最後に *NODE FILE カードで温度が.frdファイルに、*NODE PRINT カードで流体温度が.datファイルに出力されるようにします。

完全な入力デッキはCalculiXのテスト例に含まれています（furnace.inp）。 この解析では2番目のステップは追加され、追加の3000秒の間、底面の温度が一定となるようになっています。

計算中に何が起きるでしょうか？　壁の熱伝導と底面からの輻射によって加熱炉の壁と上面は熱せられます。 しかし同時に上面は外部への輻射と流体との対流によって熱を失います。 流体との相互作用によって温度の対称性は破れます。 流体の温度が高くて加熱炉との温度差が小さい流出部よりも、流体が冷たい流入部で加熱炉は多くの熱を失うでしょう。 従って対流によって温度は流入部から流出部に向かって増加するはずです。 また熱伝導によって温度は上部の中央で最小になるはずです。 両方の効果が重なりあった結果、t=3001s での温度分布は図18 に示すようになります。加熱炉底部から上部に向かって温度勾配ができあがり、上部の温度は確かに対称ではありません。 位置A、B、C、D、Eの温度を時間に対してプロットすると図19 の様になります。

定常状態にはまだ到達していないことに注意してください。 また（シェル要素などの）2D要素が自動的に正しい厚みの3D要素に拡張されていることにも注意が必要です。 CalculiX GraphiXで描画された図では3D要素が図示されているのはこのためです。

次へ 上へ 前へ 目次へ
次へ：Seepage under a dam 上へ：Simple example problems 前へ：Frequency calculation of a 目次へ
guido dhondt 2016-03-08