 |
**
** Structure: slender disk mounted on a long shaft
** Test objective: *COMPLEX FREQUENCY.
**
*NODE, NSET=Nall
1,6.123233995737e-17,1.000000000000e+00,0.000000000000e+00
...
*ELEMENT, TYPE=C3D20R, ELSET=Eall
1, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
11, 12, 17, 18, 19, 20, 13, 14, 15, 16
...
*NSET,NSET=Nfix
14,
136,
...
*BOUNDARY
Nfix,1,3
*Solid Section, elset=Eall, material=steel
*Material, name=STEEL
*Elastic
210000., 0.3
*DENSITY
7.8e-9
*Step,nlgeom
*Static
*dload
Eall,centrif,3.0853e8,0.,0.,0.,0.,0.,1.
*end step
*step,perturbation
*frequency,STORAGE=YES
10,
*end step
*step
*complex frequency
10,
*NODE FILE
PU
*end step
E I G E N V A L U E O U T P U T
MODE NO EIGENVALUE FREQUENCY
REAL PART IMAGINARY PART
(RAD/TIME) (CYCLES/TIME) (RAD/TIME)
1 -0.471037E+08 0.0000000E+00 0.0000000E+00 0.686321E+04
2 -0.471037E+08 0.0000000E+00 0.0000000E+00 0.686321E+04
3 0.2240062+09 0.1496684+05 0.2382046E+04 0.0000000E+00
4 0.2240062+09 0.1496684E+05 0.2382046E+04 0.0000000E+00
5 0.9466374E+09 0.3076747E+05 0.4896795E+04 0.0000000E+00
6 0.9466374E+09 0.3076747E+05 0.4896795E+04 0.0000000E+00
7 0.2028547E+10 0.4503940E+05 0.7168243E+04 0.0000000E+00
8 0.2930439E+10 0.5413353E+05 0.861561E+04 0.0000000E+00
9 0.2930439E+10 0.5413353E+05 0.861561E+04 0.0000000E+00
10 0.5367484E+10 0.7326312E+05 0.1166019E+05 0.0000000E+00
P A R T I C I P A T I O N F A C T O R S
MODE NO FREQUENCY
REAL PART IMAGINARY PART
(RAD/TIME) (CYCLES/TIME) (RAD/TIME)
1 0.3179491E+04 0.5060316E+03 0.3031618E-03
2 0.8499901E+04 0.1352801E+04 -0.2864205E-04
3 0.1481488E+05 0.2357861E+04 -0.1108269E-02
4 0.2307301E+05 0.3672184E+04 -0.3240550E-04
5 0.2634670E+05 0.4193207E+04 0.1973187E-04
6 0.4102791E+05 0.6529794E+04 0.8690869E-04
7 0.4503940E+05 0.7168244E+04 0.2343947E-06
8 0.4649931E+05 0.7400595E+04 0.6623206E-04
9 0.6262165E+05 0.9966545E+04 0.5469548E-04
10 0.7375084E+05 0.1173781E+05 0.2650943E-05
これは複素周波数計算の例です。外径10、内径2、厚み0.25の円盤が、外径2、内径1の細いシャフトに取り付けられています(テスト例の rotor.inp)。円盤はシャフトの中央に取り付けられ、末端は全方向に対して固定されています。ディスクのそれぞれの端からのシャフトの長さは50です。この例の入力デッキは図11の通りです。
デッキは節点と要素の定義から始まります。セットNfixにはシャフト末端の節点が含まれ、それらは全方向に対して固定されています。材質はごく普通の鉄です。遠心荷重のために密度が必要になることに注意してください。
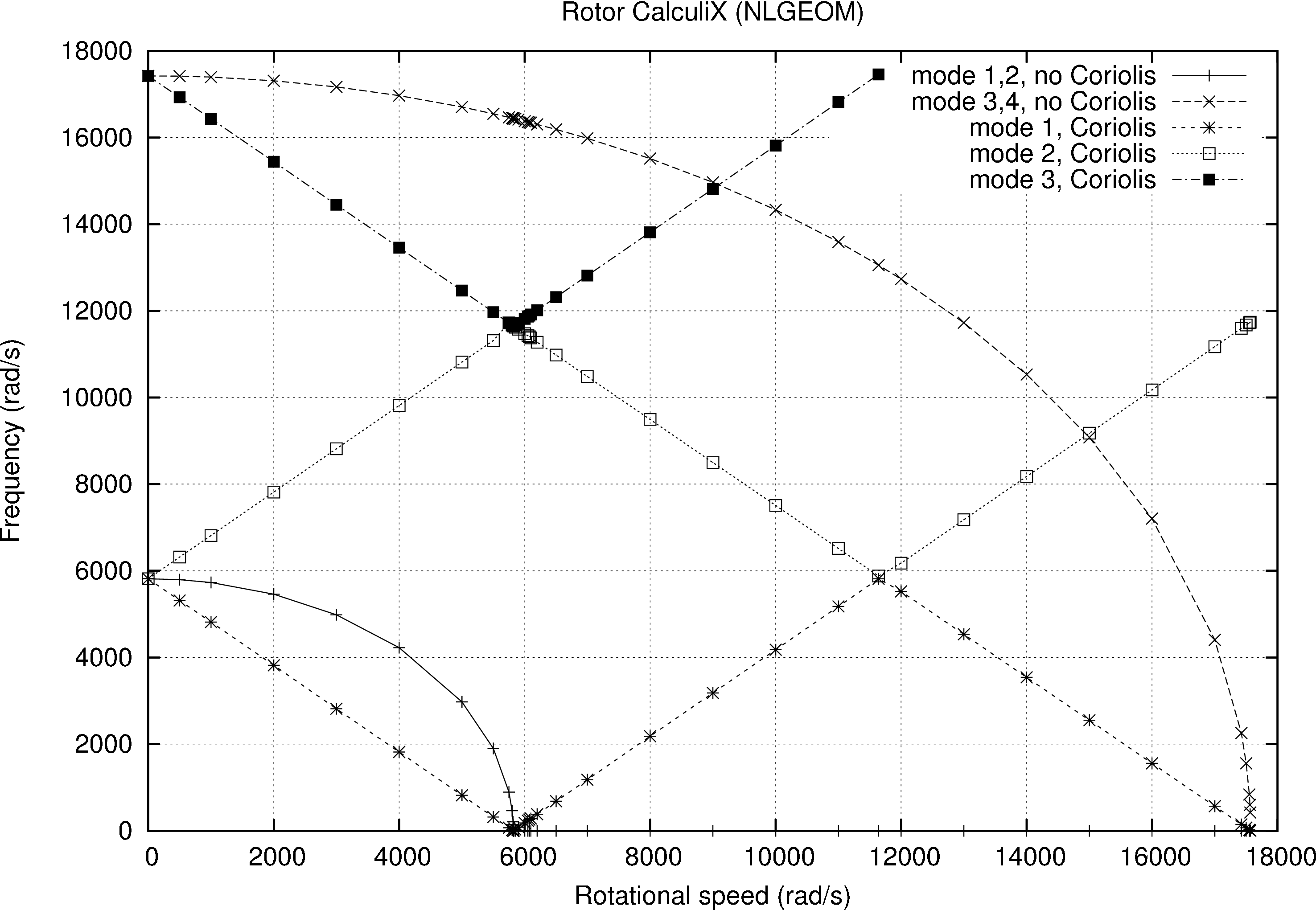
円盤は回転しているので遠心力の形であらかじめ荷重がかかっています。従ってこの荷重による変形と応力を計算するために最初のステップは 非線形の幾何静的ステップになります。後のFREQUENCYステップでPERTUBATION(摂動)パラメーターを選択すると、周波数計算での剛性行列の計算にこの事前にかけた荷重の効果が取り入れられます。計算結果の固有周波数はrotor.dat(図12。回転速度9000 rad/sの結果)の上部に記載されます。*FREQUENCYステップで固有値問題が解かれ、その固有値(図12の最上部の1列目)は構造体の固有周波数の2乗(2列目から4列目)になることがわかります。固有値が負の数の場合、結果は虚周波数になります。回転体を9000rad/sで回転させた場合の下から2つの固有値がこれにあたります。シャフトの速度が6000rad/sのあたりを下回る場合には固有周波数は実数になります。18000rad/sまでの回転速度に対する最低の固有周波数を関数として図示すると図13(+とxの曲線)のようになります。
虚周波数の物理的な意味とは何でしょう?周波数計算の結果得られた固有値にはeiωtという項が含まれています。固有周波数ωが実数の場合、これはサインまたはコサインになります。一方でωが虚数の場合、これは増加または減少する指数関数[18]になります。つまり、虚周波数について言えばその応答はもはや振動ではないのです。系が破壊されるまで増加し続けるのです。図13を見るとシャフト速度が上昇するとともに最低の固有周波数が減少し、シャフト速度が6000rad/sのあたりでゼロ点に達していることがわかります。その点で固有周波数は虚数になり、回転体は分解します。これは長い間、エンジニアたちを悩ませました。現実の系は分解されずに超臨界の速度に達してしまうのです。
ここで重要なのはこの計算が(シャフトに対して固定された)回転座標系で行われているということです。加速系ではニュートンの法則は破れますが、回転座標系は加速されているのです。コリオリ力の形でニュートンの法則に対する補正項が必要なのです。コリオリ力を導入することで複素非線形固有値系になり、*COMPLEX FREQUENCYプロシージャを使って解けるようになります(参照:セクション6.9.3)。これで結果の周波数は実数になりますが、固有値は通常は複素数になります。これが回転の固有モードです。
*COMPLEX FREQUENCYプロシージャを使うためにはコリオリ力無しで固有値を計算しそれを前の*FREQUENCYステップで保持しておく(STORAGE=YES)必要があります(参照:図11)。複素周波数応答はこれらの固有モードの線形結合として計算されます。*COMPLEX FREQUENCYステップで要求される固有周波数の数はこの先行する*FREQUENCYステップのそれを超えてはいけません。固有モードは複素数なので、*NODE FILEカードの下のPUで振幅と位相として保持するのが適しています。
回転シャフトの正しい固有値からは図13の直線が導かれます。 それぞれの直線は固有モードを表しています。一番下の減少する直線は2節点の、-z軸に対して反時計回りの(ccw)固有モード、 一番上の減少する直線は3節点のccw固有モード、上下の増加する直線は両方とも2節点の時計回り(cw)の固有モードです。 節点とは半径方向の動きがゼロになる位置のことです。 図14では2節点、図15では3節点の固有モードを示しています。 図13のX軸、Y軸のスケールが同じ場合には、この直線が45°より下になることに注意してください。
増加する直線の両方が同じ固有値と対応することに驚くかもしれません。 例えばシャフト速度が5816 rad/s の時には固有周波数 0 rad/s と固有周波数 11632 rad/s で同じ固有モードが生じます。 しかし思い出してください。固有モードは回転系で計算されている、つまりシャフトとともに回転している観測者によって観測されているのです。 止まった観測者にとっての周波数を得るには原点を通過し図を2分する45°の直線に対する相対値として周波数を考える必要があります。 この観測者から見るとそれぞれの固有モードは 5816 rad/s と -5816 rad/s、そう時計回りと反時計回りです。
最後に、コリオリ効果は常に相対的というわけではありません。 一般的に言って細長い回転構造物(大きな刃など)はコリオリ効果によって大きな周波数シフトを起こします。