ビーム・ノット

ひとつのビーム節点が拡張されると平面状に節点セットが生まれます。従ってこの拡張によるノットの伸縮はその平面上にある2つの主方向に沿った伸縮に還元できます。ビーム軸方向の伸縮は関係してきません。T₁ がローカルなビーム軸方向の単位ベクトル、E₁、E₂が拡張平面上にある2つの単位ベクトルでE₁・E₂=0 かつ E₁×E₂=T₁ だとしましょう。この時、平面内での伸縮はその主方向に沿ったベクトル T₂ とベクトル T₃ で特徴づけられます。

ここで3つの伸縮自由度 φ 、ξ 、η が現れます。φ は T₂ と E₁ のなす角、ξ は T₂ に沿った伸縮、η は T₃ に沿った伸縮です。ここから右ストレッチテンソル U は以下の様に書くことができます。

U	= T₁⊗T₁ + T₂⊗T₂ + T₃⊗T₃
	= T₁⊗T₁ + (ξ²cos²φ + η²sin²φ)E₁⊗E₁ + (ξ²cos²φ + η²sin²φ)E₂⊗E₂
	+(ξ²-η²) cosφ sinφ (E₁⊗E₂ + E₂⊗E₁)	(50)

ここで θ は θ=θn、 $\Vert\boldsymbol{n}\Vert=1$ を満たす回転軸に沿ったベクトルです。また計算におけるある点でのノットを (w₀, θ₀, φ₀, ξ₀, η₀)、その変位を (Δw, Δθ, Δφ, Δξ, Δη) で表すと以下の様になります（式（46）を参照）。

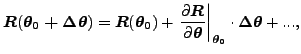$\displaystyle \boldsymbol{R} (\boldsymbol{\theta_0+\Delta \theta})=\boldsymbol{... ...}} \right \vert _{\boldsymbol{\theta_0}} \cdot \boldsymbol{\Delta \theta}+ ...,$

(53)

U についても同様で、1次の項のみを残すと次の式が導かれます。

$\displaystyle \boldsymbol{\Delta u }=$	$\displaystyle \boldsymbol{\Delta w}+\left[ \left. \frac {\partial \boldsymbol{R... ... \boldsymbol{U}(\varphi_0, \xi_0, \eta_0) \cdot (\boldsymbol{p}-\boldsymbol{q})$
	$\displaystyle + \boldsymbol{R} (\boldsymbol{\theta_0}) \cdot \left[ \left. \fra... ...right \vert _{\eta_0} \Delta \eta \right] \cdot (\boldsymbol{p}-\boldsymbol{q})$
	$\displaystyle + \boldsymbol{w_0}+[\boldsymbol{R} (\boldsymbol{\theta_0}) \cdot ... ...ta_0) - \boldsymbol{I}] \cdot (\boldsymbol{p}-\boldsymbol{q})-\boldsymbol{u_0}.$	(54)

この後者の式はノットに属する任意節点の変位の変化とノットのパラメーターの変化（平行移動、回転、伸縮）を結びつける非同次線形方程式です。この式は支配方程式の立式過程を考慮されています。この時、従属する拡張対象の自由度は解かれる式に1度も現れません。