次へ 上へ 前へ 目次へ
次へ：Arbitrary knot 上へ：Mathematical description of a 前へ：Beam knot 目次へ

シェル・ノット

1つのシェル節点が拡張されると直線上に並ぶ節点セットが生まれます。従ってストレッチテンソル U はこの直線に沿った伸縮に還元されます。T1 をこの拡張に平行な単位ベクトル、T2 と T3 を T2・T3=0 かつ T1×T2=T3 であるような単位ベクトルとすると、U は以下の様に書くことができます。

$\displaystyle \boldsymbol{U}=\alpha \boldsymbol{T_1} \otimes \boldsymbol{T_1}+\boldsymbol{T_2} \otimes \boldsymbol{T_2}+\boldsymbol{T_3} \otimes \boldsymbol{T_3}$ (55)

ここでひとつの伸縮パラメーター α が現れます。T2 と T3 に沿った伸縮は無視できるので式（55）は等方的な拡張を表す以下の式で置き換えることができます。

$\displaystyle \boldsymbol{U}=\alpha \boldsymbol{T_1} \otimes \boldsymbol{T_1}+\... ...l{T_2}+\alpha \boldsymbol{T_3} \otimes \boldsymbol{T_3} = \alpha \boldsymbol{I}$ (56)

式（54）は以下の式で置き換えることができます。

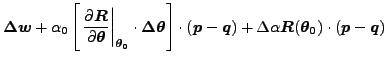$\displaystyle \boldsymbol{\Delta u }=$ $\displaystyle \boldsymbol{\Delta w}+\alpha_0 \left[ \left. \frac {\partial \bol... ...ha \boldsymbol{R} (\boldsymbol{\theta_0}) \cdot (\boldsymbol{p}-\boldsymbol{q})$
$\displaystyle + \boldsymbol{w_0}+[\alpha_0 \boldsymbol{R} (\boldsymbol{\theta_0}) - \boldsymbol{I}] \cdot (\boldsymbol{p}-\boldsymbol{q})-\boldsymbol{u_0}.$ (57)

結果、シェルの拡張によって生まれるノットは3つの平行移動自由度、3つの回転自由度、1つの伸縮自由度で特徴づけられます。

次へ 上へ 前へ 目次へ
次へ：Arbitrary knot 上へ：Mathematical description of a 前へ：Beam knot 目次へ
guido dhondt 2016-03-08