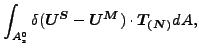 |
(125) |
面・面ペナルティー接触の弱形式の寄与は[18]の式(2.6)の右辺第1項にと対応し、スレーブ側、マスター側の両方について書き表されます。これは(物体座標系では)以下の様になります。
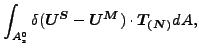 |
(125) |
また空間座標系では以下の様になります。
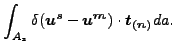 |
(126) |
t(n) でテイラー展開すると、これは us-um の関数になって1次の項のみが残り(差分変位がゼロの場合は摩擦力がゼロになるので定数項は消えます)次の式を得ることができます。
積分範囲がスレーブ面であることに注意してください。マスター側の対応する位置はローカルな正射影によって得られます。スレーブ側での面内の変位は面に属する節点の変位の線形結合として書き表すことができます(ns はスレーブ面に属する節点の数です)。
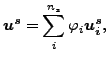 |
(128) |
マスター側の変位も同様です(![]() はマスター面 ml に属する節点の数です)
はマスター面 ml に属する節点の数です)
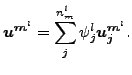 |
(129) |
上式を式(127)に代入すると以下が得られます。
![$\displaystyle \sum_{s} \sum_{i=1}^{n_s} \sum_{j=1}^{n_s} \delta \boldsymbol{u_i...
...}}}{\partial \boldsymbol{u^s} } \varphi _j da \right ] \cdot \boldsymbol{u_j^s}$](img669.png) |
||
| - | ![$\displaystyle \sum_{s} \sum_l \sum_{i=1}^{n_s} \sum_{j=1}^{n_m} \delta \boldsym...
...{\partial \boldsymbol{u^s} } \psi _j^l da \right ] \cdot \boldsymbol{u_j^{m^l}}$](img671.png) |
|
| - | ![$\displaystyle \sum_{s} \sum_l \sum_{i=1}^{n_m} \sum_{j=1}^{n_s} \delta \boldsym...
...}}}{\partial \boldsymbol{u^s} } \varphi _j da \right ] \cdot \boldsymbol{u_j^s}$](img672.png) |
|
| + | ![$\displaystyle \sum_{s} \sum_l \sum_{i=1}^{n_m} \sum_{j=1}^{n_m} \delta \boldsym...
...\partial \boldsymbol{u^s} } \psi _j^l da \right ] \cdot \boldsymbol{u_j^{m^l}}.$](img673.png) |
(130) |
ここで「![]() 」はスレーブ面 s の一部で、この正射影はマスター面 ml に含まれます。これによって次の剛性寄与が導かれます(符号の変化に注意してください。弱項は[18]の式(2.6)の左辺に移動しなければならないのです)。
」はスレーブ面 s の一部で、この正射影はマスター面 ml に含まれます。これによって次の剛性寄与が導かれます(符号の変化に注意してください。弱項は[18]の式(2.6)の左辺に移動しなければならないのです)。
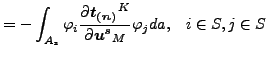 |
(131) | |
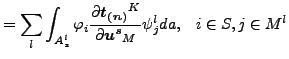 |
(132) | |
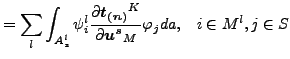 |
(133) | |
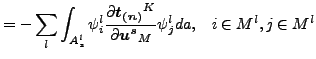 |
(134) |
S は今問題にしているスレーブ面「s」、Ml は 無限小のスレーブ領域 da の正射影が属するマスター面です。上式の積分は数値積分によって評価されます。例えばスレーブ面の古典的ガウス点を使用することができます。しかしこれでは精度のよい結果を得ることはできません。マスター面とスレーブ面が対応せず、積分関数の導関数が不連続なためです。図116で描かれる、前のセクションで示されている積分法を使うともっと良い結果を得ることができます。この方法を使うと上記の積分は以下の様に置き換えられます。
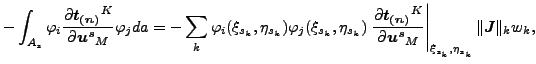 |
(135) |
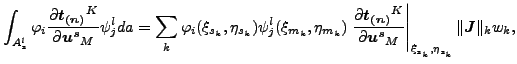 |
(136) |
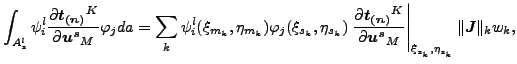 |
(137) |
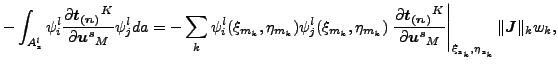 |
(138) |
ここで k は積分点の数、(ξsk, ηsk)はスレーブ積分点のローカル座標、(ξmk, ηmk)はスレーブ積分点をマスター表面に正射影した時のマスター面上でのローカル座標、![]() はスレーブ面状の積分点でのローカルなヤコビ・ベクトルのノルム、wk は重みです。先に述べたように同じスレーブ面内の積分点の投影は異なるマスター面に所属することがあります。各スレーブ積分点 k はスレーブ面とマスター面をつなぐ接触要素を生み出し、上記の積分点 k の値の式で表現される寄与から作成されるサイズ 3(ns + nm)×3(ns + nm) の剛性行列によって表されます。
はスレーブ面状の積分点でのローカルなヤコビ・ベクトルのノルム、wk は重みです。先に述べたように同じスレーブ面内の積分点の投影は異なるマスター面に所属することがあります。各スレーブ積分点 k はスレーブ面とマスター面をつなぐ接触要素を生み出し、上記の積分点 k の値の式で表現される寄与から作成されるサイズ 3(ns + nm)×3(ns + nm) の剛性行列によって表されます。
以上から、完全な接触要素の剛性行列を得るためにはスレーブ積分点での3×3の剛性行列
を決定すれば十分であることが分かります。これはスレーブ面上の積分点で静止摩擦を同じ位置での変位ベクトルで微分したものです。