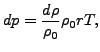準静的計算のための理想気体

線形等方弾性材料の特殊な例が微小圧力変動下の理想気体です。理想気体方程式から圧力変動 dp は密度変化 dρ と以下の関係を持つことがわかります。

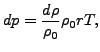(152)

ここで ρ₀ は静止状態での密度、r は比気体定数、T は絶対温度です。この式から次の式を導くことができます。

ここで t は応力を、ε は線形ひずみを意味します。つまり理想気体はラメ定数 λ=ρ₀rT、μ=0 を持つ等方性の弾性材料としてモデル化できるということです。これはヤング率 E=0 、ポアソン係数 ν=0.5 と対応するものです。後者の値には数値的困難さがあるため、理想気体を D₁₁₁₁=D₂₂₂₂=D₃₃₃₃=D₁₁₂₂=D₁₁₃₃=D₂₂₃₃=λ と D₁₂₁₂=D₁₃₁₃=D₂₃₂₃=0 を持つ等方性材料として定義する方法には利点があるのです。