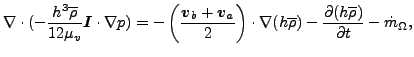 |
(208) |
流体潤滑では、停止側部品とベアリングなどの高速回転部品との間に薄い油膜が校正されます。工学的に主な問題になるのは圧力で表される薄膜の耐荷重能力です。流体方程式を薄膜の厚み方向に積分すると以下のような方程式が求まります[26]。
ここで h は膜の厚み、![]() は厚み方向の平均密度、μv は流体の動粘性係数、va は膜の片側での速度、vb は膜のもう片側での速度、
は厚み方向の平均密度、μv は流体の動粘性係数、va は膜の片側での速度、vb は膜のもう片側での速度、![]() は多孔質の壁を通って膜から流出(流出時にプラス)する結果体積流量(体積/秒/単位面積)です。壁が多孔質体でない場合はこの値はゼロです。
は多孔質の壁を通って膜から流出(流出時にプラス)する結果体積流量(体積/秒/単位面積)です。壁が多孔質体でない場合はこの値はゼロです。
現実的な計算では膜の密度と厚みは既知、圧力は未知と考えられます。熱方程式と比較すると、その対応関係は表(11)の様になります。
![]() は膜全体での平均速度、
は膜全体での平均速度、![]() は境界に垂直なその成分です。支配方程式は膜厚み方向の積分の結果なので、再び2次元になり、現在の形から平らな膜へと変わります。さらに定常状態方程式(右側の密度の時間変化が既知)だとすると、この式はポアソン方程式になります。ここでも浅水方程式同様、空間変動する層厚みは熱伝達での空間変動する伝導係数と等価です。
は境界に垂直なその成分です。支配方程式は膜厚み方向の積分の結果なので、再び2次元になり、現在の形から平らな膜へと変わります。さらに定常状態方程式(右側の密度の時間変化が既知)だとすると、この式はポアソン方程式になります。ここでも浅水方程式同様、空間変動する層厚みは熱伝達での空間変動する伝導係数と等価です。