平均回転 MPC

この MPC は節点セットに回転を適用するために使用されます。回転は大きさ（ラジアン単位の角度）と軸（法線ベクトル）で特徴づけられます。回転に関与する節点は全て（各自由度ごとに1度ずつ）3回リストアップされる必要があります。ユーザーは回転の大きさと軸を定義するための追加節点を最後に定義しなければなりません。追加節点の座標は回転軸ベクトルの各成分で、節点の最初の自由度が回転の大きさとして解釈されます。この大きさは *BOUNDARY カードを使用して定義することができます。平均回転の適用は、個別の回転それ自体ではなく、関与する全節点の平均回転量が指定された値となることを意味します。平均回転の補完物が回転に必要なトルクです。*NODE PRINT カード、または *NODE FILE カードで RF を選択するとこのトルクを .dat または .frd ファイルに保存することができます。これを使用すると、平均回転を指定する代わりにトルクを適用し（塚節点の最初の自由度に *CLOAD を使用して力を指定）、平均回転結果を計算をするk十が可能です。

非線形方程式が長くなるに従って平均回転 MPC に含まれる節点は増えます。これによって方程式系に巨大で稠密なサブ行列が生じ、解析時間が長くなっていきます。従っておおよそ50を超える節点を平均回転 MPC に含めないよう推奨します。

例：
*NODE
162,0.,1.,0.
*MPC
MEANROT,3,3,3,2,2,2,14,14,14,39,39,39,42,42,42,
50,50,50,48,48,48,162
..
*STEP
*STATIC
*BOUNDARY
162,1,1,.9
..
*END STEP

上記では平均回転 MPC を指定しています。大きさは0.9ラジアン=51.56°で回転軸はグローバル Y 軸です。対象となる節点は3、2、14、39、42、50、48です。

サンプルファイル: beammr、beammrco

平均回転 MPC の背景にある理論は[18]、セクション3.6で説明されています。これら説明では全ての節点が回転軸に垂直な平面上にある場合について扱っています。そうでない場合には [18]での導出は正しくなく、拡張を行なう必要があります。一般化する場合には参照先の式（3.98）で P_i' と u_i' を、回転軸 a に垂直な平面に投影したものに置き換える必要があります。ベクトル y の投影 Py は以下によって与えられます。

(361)

と定義すると、参照先の式（3.101）は以下で置き換えられます（このセクションでは暗黙のサムネーションは使用していません）。

(362)

（ベクトルに自分自身をかけ合わせると消えることを思い出してください）。λ_i はとの間の角度の sin で、平均回転 MPC がその節点 i に適用される節点セットの重心からの投影ベクトルです。または重心の変形位置と節点 i の変形位置をつなぐベクトルの投影です。平均回転 MPC の平均回転は与えられた角度 γ と等しい、つまり方程式は以下を満足するとします。

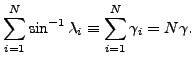(363)

線形化の係数を見つけるために、ここでに注目してみます。すると次のような関係に容易に気がつくでしょう。

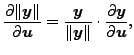(364)

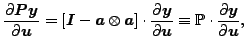(365)

(366)

さらにから、以下を得ます。

(367)

最後に以下（参照先の式（3.96））から

(368)

次を得られます。

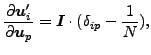(369)

ここで I は単位2次制度テンソルです。上の式を使用すると以下が得られます。

(370)

(371)

これで参照先の式（3.109）を置き換えます。