 |
1次元要素、2次元要素と3次元要素の間の接続はサブルーチン「gen3dconnect.f」で行なわれますが、ここでも特別な注意が必要です。拡張された要素は新しい節点だけで構成されるので、ユーザーによって入力デッキで定義されたそれら要素と3次元要素の間の接続は失われます。多点拘束を作成することで接続を復元する必要があるのです。ただしこれはノットに対しては当てはまりません。ノットでは、元節点を並進節点として使用して拡張可能な剛体が定義されます(ノットは並進節点、回転節点、拡張節点によって定義されることを思い出してください)。従ってノットの場合には3次元要素との接続が保証されます。以下はノットが定義されていない節点に対して成り立つものです。
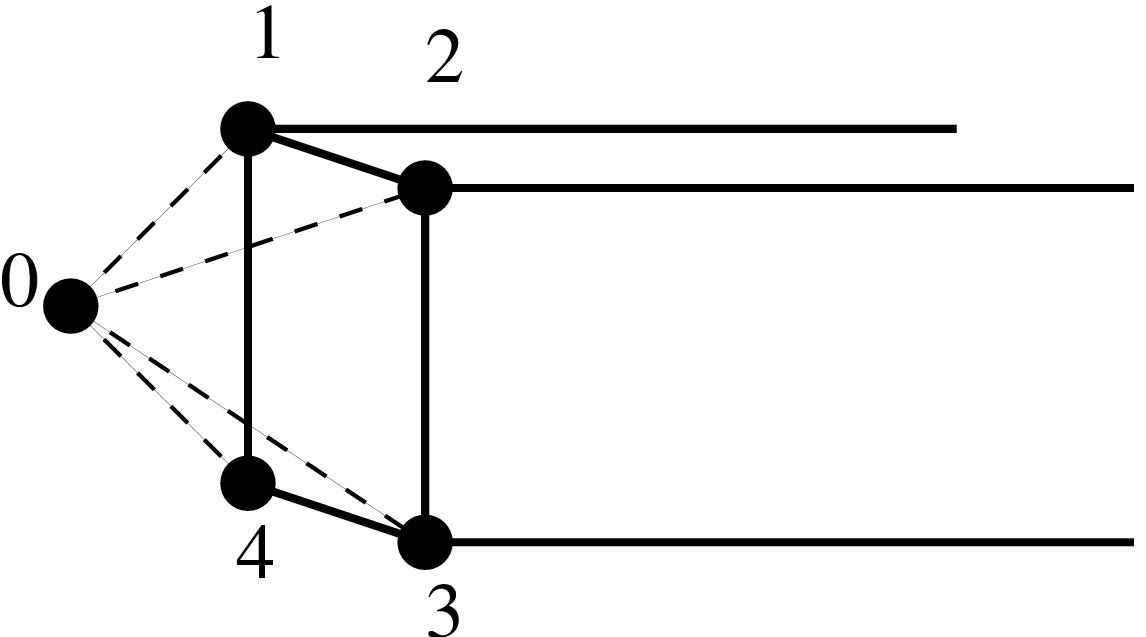
1次元ビーム要素では接続は以下の方程式によって表されます(節点番号に関しては図138を参照)。
ここで u は任意の変位成分(または熱伝達計算における温度成分)で、上式は実際は機械問題においては3方程式を、熱伝達問題では1方程式を、熱機械問題では4方程式を表しています。使用されているのがビーム要素の端節点だけであることに注意してください。つまりビーム要素の中間節点に対して適用することもできるのです。この式は3次元節点の変位が拡張された端節点の変位の平均となることを表しています。
2次元シェル要素では接続は以下の方程式によって表されます(節点番号に関しては図139を参照)。
ここでもビーム要素と同じ説明が当てはまります。
平面ひずみ要素、平面応力要素、軸対称要素では接続は図140、以下の方程式に従って作成されます。
節点1は拡張された要素のゼロ Z 節点です。20節点ブリック要素は、元の2次元要素の節点と対応するゼロ Z 節点を使用しませんが、それらは存在し、上式の様に MPC で使用することができます。接続は最終的には上記の MPC と、ゼロ Z 節点と負・正 Z 節点をつなぐ平面ひずみ要素、平面応力要素、軸対称要素 MPC の組み合わせによって設定されます。