第十二類 近似並行運動 Approximate Parallel Motion.
本類は実用上使用に差支えなき程度に近似並行運動を為す機構を集む。前類において説明せる並行運動よりも構造簡単なるを以て利用せらるる場合多し。近似直線運動の別名あり。
275. ケムブ・ツエビセフ近似並行運動 “Kempe and Tchebicheff” Parallel Motion.
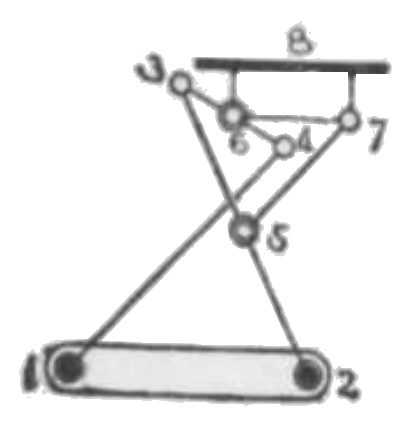
1234 はツエビセフ近似並行運動なり。(283) を見よ。
67=(1/2)×12, 57=53=52
3, 5, 2 及び 3, 6, 4 はそれぞれ一直線上にあり。
テーブル 8 はリンク 67 に並行なり。8 は左右近似直線運動と為す。
276. スコット・ラッセル近似並行運動 “Scott Russell” Parallel Motion.

三点 2, 3, 4 一直線上にあり。13:23=23:34, 5, 6 は滑りツガイにして 2 の中心の描く滑り子ツガイの軸線は 1 の中心を通過す。点 4 は近似直線を描く。ただし特別の場合として点 3 が 24 の中点なるときは点 4 は純直線を描く。
277. イナゴ型近似並行運動 Grasshopper Parallel Motion.

上述のスコット・ラッセル近似並行運動の滑り子のピン 2 の左右運動はその行長短きにより滑り子を廃して本図の如くリンク 25 の上端の弧運動に換置す。点 4 は上下に近似並行運動を為す。
278. ワット近似並行運動(其一)“Watt” Parallel Motion.
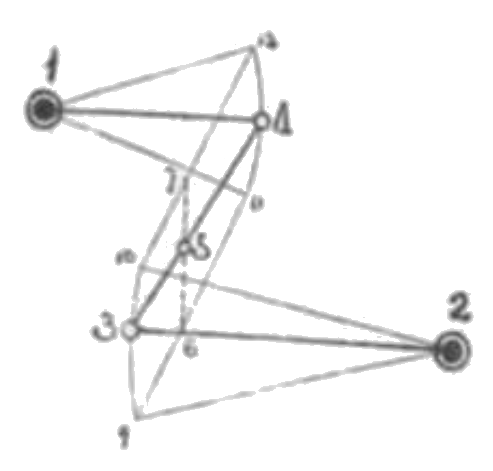
53:24=14:23
図において 14 を 23 に並行の位置に置く。然るときは両者が上下に振る場合に点 5 は近似直線を描く。
英人ワットが初めて汽機にこの機構を用いたるを以てこの名あり。(294) を見よ。リンク 14, 23 が相等しきときは点 5 はリンク 34 の中点なり。
279. 同(其二)
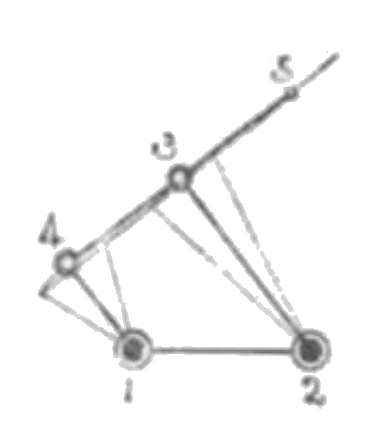
53:54=14:23
図においてリンク 14, 23 が並行なるとき両者がリンク 34 と直角を為す様に仕組む。然るときは両者が左右に振る場合に点 5 は近似直線を描く。
280. ワット近似並行運動の併用
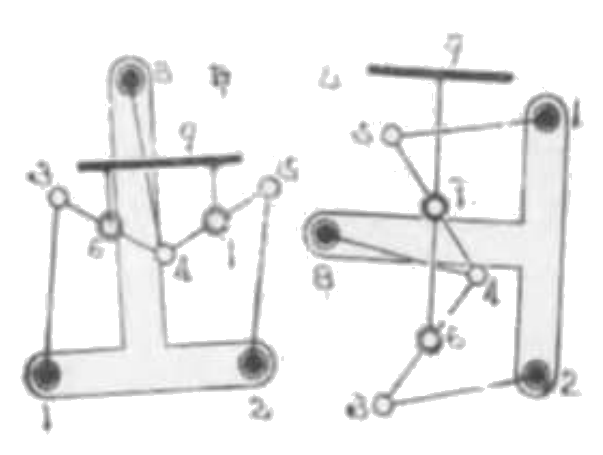
甲、乙何れも相等しき二個の並行運動を併用す。甲図においては 12 に並行なる台 9 は左右に直線之動をなし乙図においては台 9 は上下に直線運動を為す。
281. ワット近似並行運動応用のコロ
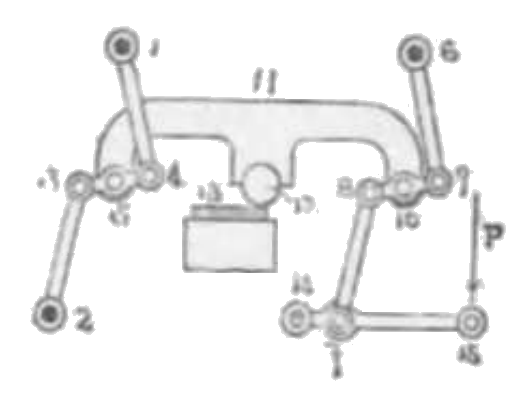
リンク 14, 23, 78, 69 は相等しく 1234, 6789 は何れもワット近似並行運動なり。コロ 12 を支うる片 11 は左右に直線運動を為すによりコロは金属板 13 を圧し延ばす。踏板 15 に加えられたる力はコロ 12 の強き圧力となる。英蘭銀行にて焼入られたる鋼製彫刻版を複成するに用いたり。
282. ロバート近似並行運動 “Rovert” Parallel Motion.
| 14, 47 の長 | 23 の長 | △235 の高さ |
|---|---|---|
| 1 | 0.667 | 3.950 |
| 1 | 0.577 | 1.100 |
| 1 | 0.500 | 0.943 |
| 1 | 0.414 | 0.654 |
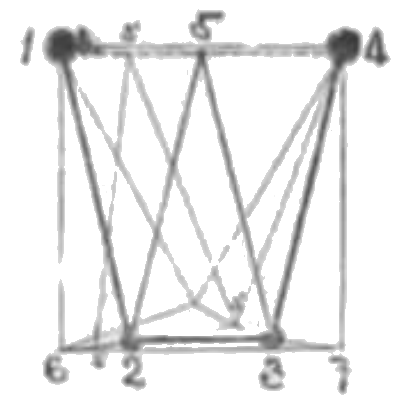
12=34, 253 は二等辺三角形。適当なる各部の寸法にて点 5 が直線 14 に並行なる直線を描く。12534 は英字 W に似たるを以てダブリュー並行運動の別名あり。
その一例: 1476 は正方形。2, 3 は辺 67 の四等分点。点 5 は辺 14 の二等分点。
英人ウィリースの与えたる各部の寸法: 14=12=43 ならしめ、25=35 なる二等辺三角形を描き、その高さ及び底辺 23 を左表の如くす。
英人ロバートの与えたる各部の寸法: 14=1, 23=0.593, △ 235 の高さ=1.112, 角 253=30°, 12=34=0.584.
283. ツェビセフ近似並行運動 “Tchebicheff” Parallel Motion.
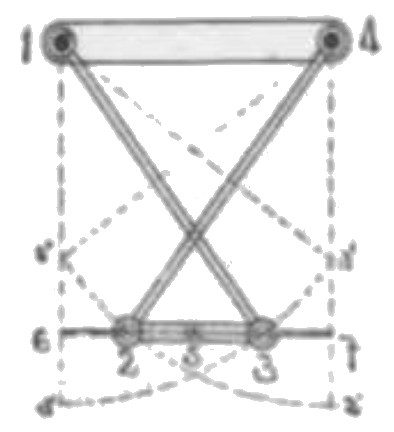
1674 は正方形。点 2, 5, 3 は辺 67 の四等分点。リンク 1324 を作る。リンク 14 を固定するときは点 5 は近似直線 67 を描く。西暦 1873 年、露国大学教授ツェビセフ初めてウィーン博覧会に出品せり。
23:14:13(又は 24)=2:4:5
284. コンコイダル近似並行運動 Conchoidal Parallel Motion.
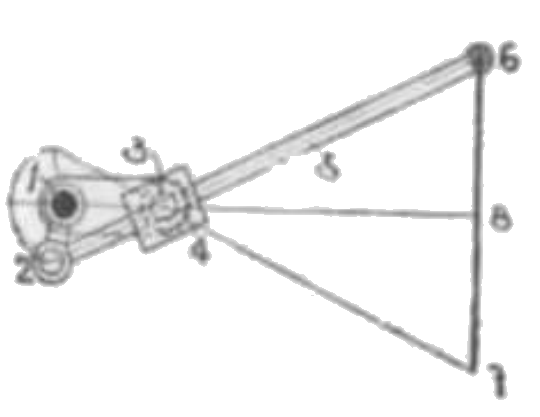
小軸 3 にて廻る滑り子 4 はロッド 5 と滑りツガイを為す。12 はクランク。然るときは棒 5 上の特種の点 6 は近似直線を描く。定長の直線 62 が定点 3 を通過し且一端 6 が与えられたる直線上に運動するときは他端 2 は点 3 において交わる環状曲線を描く之をコンコイド曲線と称す。本機構はこの環状曲線の一部をクランク 12 のピン 2 にて近似に描く様に造りたれば逆に 6 点は近似直線を描くべき理なり。
285. ルーロー近似並行運動 (其一)
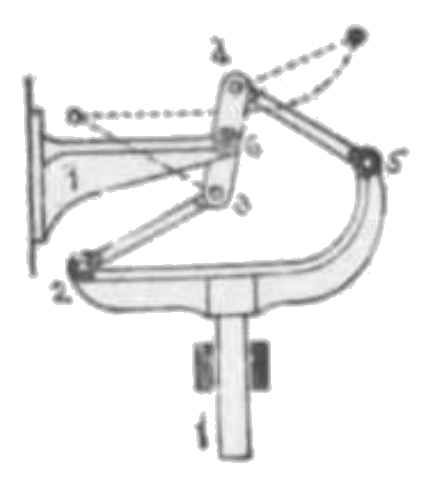
23645 はワット並行運動。上部の二枝に左右ピン 2, 5 を有するロッド 1 の中心線は点 6 を通過す。ロッド 1 は上下に直線運動を為す。之ワット並行運動の転置より得らるる機構なり。独人ルーロー機構学よりこの名を与う。
286. 同(其二)
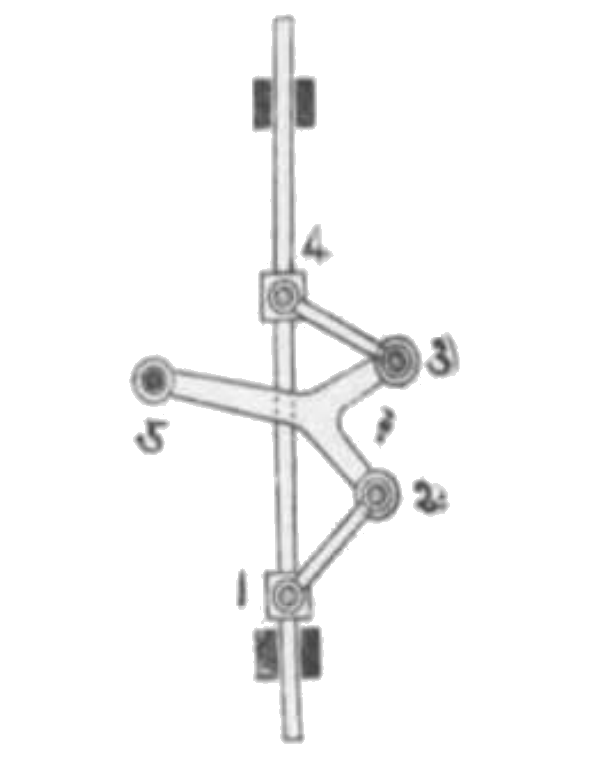
ロバート近似並行運動 (282) において 14 を固定する代わりにロッド 14 と蝶番連結し点 5 を固定するときはロッド 14 は上下に近似並行運動を為す。之転置によりてロバート近似並行運動より得たる新機構なり。
287. 同(其三)ライヘンバッハ近似並行運動 “Reichenbach” Parallel Motion.
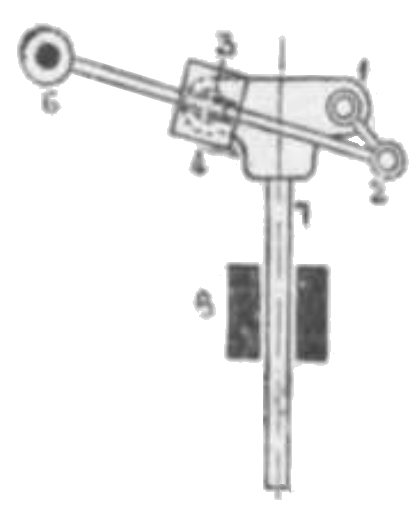
機構 (284) においてロッド 5 の右端 6 にピンを作りて固定せしめ 5 が之を中心として振動する様にす。リンク 13 に直角に取付けたるロッド 7 は上下に近似並行運動を為す。
288. リンクによる近似直線運動の案出
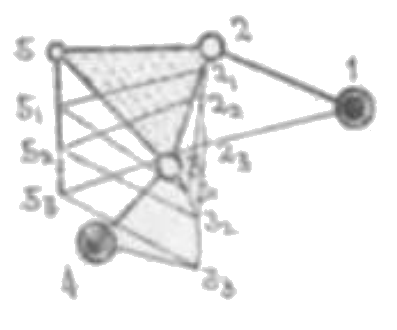
ピン 1 を固定し △235 とリンク 12 の結合ピンを 2 とし頂点 5 の動く直線路を 553 としその間に二点 51, 52 を取る。点 5 が直線 552 上に、点 2 が中心 1, 半径 12 の円弧上にある様に △235 を移して点 3, 31, 32, 33 を得。之等諸点を近似に通過する円弧を描きその中心 4 を固定す。リンク機構 1234 は求むる機構なり。