OpenMDAO ではじめる最適化 (2/4)
OpenMDAOの基本的な仕組み
基本的な仕組み
OpenMDAOではドライバー、コンポーネント、アセンブリなどを組み合わせて解析システムを作成し、実行する。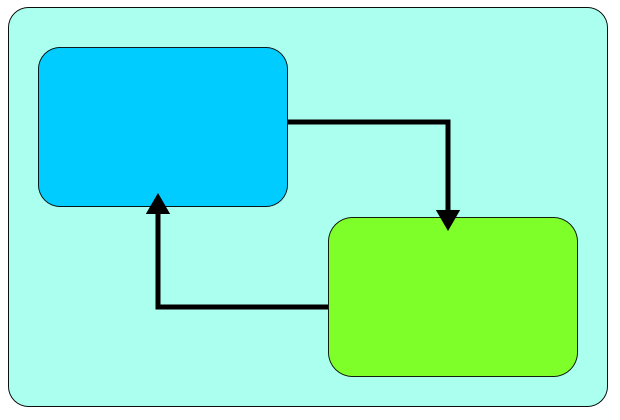
アセンブリ
コンポーネント
ドライバー
ワークフローを構成する要素にはドライバー、コンポーネント、アセンブリなどがある。
-
ドライバー
最適化用エンジン。パラメーター設定を担当。あらかじめ組み込みのものが用意されている。
入力
ドライバー
出力
-
コンポーネント
解析処理部。解く問題に応じてユーザーがPythonのクラスとして自作する。流体解析や構造解析のソルバーを使う場合はコンポーネントに組み込んで使用する。
入力
コンポーネント
出力
-
アセンブリ
処理の入れ物。アセンブリ自体をコンポーネントとして使用して階層構造を作成することも可能。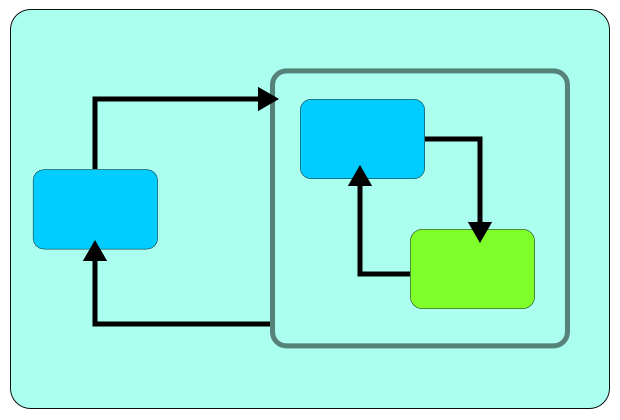
アセンブリ
アセンブリ
コンポーネントの書式
最適化したい処理を担うコンポーネントはPythonのクラスとしてユーザーが作成する。
スクリプトの内容については「スクリプトからの操作例」で説明する。 例：Paraboloid.py
スクリプトの内容については「スクリプトからの操作例」で説明する。 例：Paraboloid.py
from openmdao.main.api import Component
from openmdao.lib.datatypes.api import Float
class Paraboloid(Component):
""" f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 """
# set up interface to the framework
x = Float(0.0, iotype='in', desc='The variable x')
y = Float(0.0, iotype='in', desc='The variable y')
f_xy = Float(0.0, iotype='out', desc='F(x,y)')
def execute(self):
"""f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3
Minimum : x = 6.6667; y = -7.3333
"""
x = self.x
y = self.y
self.f_xy = (x-3.0)**2 + x*y + (y+4.0)**2 - 3.0
from openmdao.lib.datatypes.api import Float
class Paraboloid(Component):
""" f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3 """
# set up interface to the framework
x = Float(0.0, iotype='in', desc='The variable x')
y = Float(0.0, iotype='in', desc='The variable y')
f_xy = Float(0.0, iotype='out', desc='F(x,y)')
def execute(self):
"""f(x,y) = (x-3)^2 + xy + (y+4)^2 - 3
Minimum : x = 6.6667; y = -7.3333
"""
x = self.x
y = self.y
self.f_xy = (x-3.0)**2 + x*y + (y+4.0)**2 - 3.0
それでは実際の操作方法を見ていく。
例題として以下のような放物面に対して f(x, y) が最小となるよう x、 y を最適化する操作を考える。
例題として以下のような放物面に対して f(x, y) が最小となるよう x、 y を最適化する操作を考える。
放物面:
f(x, y) = (x-3)2 + xy + (y+4)2– 3
範囲:
-50 < x < 50
-50 < y < 50
初期値:
x = 10
y = 10
f(x, y) = (x-3)2 + xy + (y+4)2– 3
範囲:
-50 < x < 50
-50 < y < 50
初期値:
x = 10
y = 10