次へ 上へ 前へ 目次へ
次へ：Turbulent Flow in Open 上へ：Types of analysis 前へ：Aerodynamic Networks 目次へ


水力ネットワーク

水力ネットワークは、非圧縮性媒体で満たされたネットワーク要素（セクション6.2.31を参照）を連結して作成されます。ネットワーク要素は3つの節点から構成されます。端節点では温度と圧力は未知、中間節点では質量流量が未知です。端節点はネットワークの接続点の役割を担い、中間節点は1要素内の流れを表します。これらの未知数を決定するためには3種類の式が利用できます。端節点での質量保存式、エネルギー保存式、中間節点での運動量保存式です。今のところ対応しているのは定常流れだけです。

定常流れにおける非圧縮性流体での質量保存則は以下の形で表現されます。

$\displaystyle \mathbf{\nabla} \cdot \mathbf{v} = 0$ (248)

ここで ρ は密度、v は流速ベクトルです。端節点につながる全ての要素にわたって積分を行なうと以下の様になります。

$\displaystyle \sum_{j \in \text{in}} \dot{m}_{ij} = \sum_{j \in \text{out}} \dot{m}_{ij},$ (249)

$ \dot{m}_{ij}$は節点 i と 節点 j の間の質量流れです。上式では$ \dot{m}_{ij}$は常に正です。

運動量保存式はベルヌーイの式へ変換できます。端節点 i 、j を持つ要素内の流線上に一般的な運動量保存式を投影すればよいのです。すると以下のような式が得られます。

$\displaystyle z_i + \frac{p_i}{\rho g} + \frac{\dot{m}_{ij}^2}{2 \rho^2 A_i^2 g... ... + \frac{p_j}{\rho g} + \frac{\dot{m}_{ij}^2}{2 \rho^2 A_j^2 g} + \Delta F_i^j.$ (250)

ここで z は接点の高さ、p は圧力、ρ は密度、g は重力加速度、A は節点での断面積、$ \Delta F_i^j$は要素全体での損失水頭です。損失水頭は i から j に向かう流れの時を正、それ以外の場合を負とします（そうでない場合は式を反対に書きます）。流体セクションのタイプごとの損失水頭についてはセクション6.5で説明されています。

節点高さは重要です。従って水力ネットワークでは *DLOAD カードを使用して各要素に対して重力ベクトルを定義する必要があります。

定常状態でのエネルギー保存式は以下の様になります（[18]）。

$\displaystyle c_p \mathbf{\nabla} \cdot (\rho \theta \mathbf{v}) = - \mathbf{\nabla} \cdot \mathbf{q} + \rho h^{\theta},$ (251)

ここで q は外部の熱フラックス、$ h^{\theta}$は単位質量あたりの体積フラックス、cp は定圧比熱（流体ではこれは定積比熱でもあります。つまり$ c_p=c_v$です[25]）、θ は絶対温度（ケルビン温度）です。終端節点 i に属する全ての要素にわたってエネルギー方程式を積分した結果は以下の様になります。

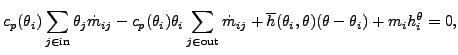$\displaystyle c_p (\theta_i) \sum_{j \in \text{in}} \theta_j \dot{m}_{ij} - c_p... ...{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0,$ (252)

$ \overline{h}(\theta_i,\theta)$は壁に対する対流係数です。ある節点に流入する全ての流れが同時に流出しなければならず、両方ともが流入する流れの平均温度値と対応する cp を持つとすると、以下の様になります。

$\displaystyle \sum_{j \in \text{in}} c_p (\theta_m) (\theta_j-\theta_i) \dot{m}_{ij} + \overline{h}(\theta_i, \theta) (\theta - \theta_i) + m_i h_i^{\theta}=0.$ (253)

ここで$ \theta_m=(\theta_i+\theta_j)/2$です。

水力ネットワークの計算は *HEAT TRANSFER キーワード・カードによって有効になります。このようなネットワークでは固体力学的な熱伝達計算のための対流境界条件が必要になることが多いですが、ネットワーク計算では独自に実行を行なうことができます。つまり固体要素なしでも *HEAT TRANSFER 計算を実行できるのです。

適切な水力ネットワークの境界条件を決定するためには、空力ネットワークと同じ規則を使用できます。

出力変数は質量流量（*NODE PRINT カードまたは*NODE FILEカードのMFキー）、全圧（*NODE PRINT カードのPNキー……Network Pressure…… と*NODE FILE カードのPSキー）、全温度（*NODE PRINT カードのNTキー、*NODE FILE カードのTTキー）です。*NODE PRINT キーワードのラベルはより一般的なもので、*NODE FILE キーワードのものはより詳細なものであることに注意してください。これら変数はネットワークにおける主要変数です。内部的には、ネットワーク節点では変位場の第1成分から第2成分がそれぞれ質量流量、静圧に使用されています。従って *NODE PRINT カードまたは *NODE FILE カードで U を使用しても出力を行なうことが可能です。

流体では全温度は実質的に静温度と一致することに注意してください。

$\displaystyle \theta_{tot}-\theta = v^2/(2c_p),$ (254)

であるため、流速5 m/s 、$ c_p=4218$ J/(kg.K)（水）の時の全温度と静温度の差は 0.0030 K になります。これは気体との大きな違いです。典型的な気体では流速がもっと速く（音速は340 m/s）、通常は cp がもっと低いからです。

次へ 上へ 前へ 目次へ
次へ：Turbulent Flow in Open 上へ：Types of analysis 前へ：Aerodynamic Networks 目次へ
guido dhondt 2016-03-08