次へ 上へ 前へ 目次へ
次へ：Three-dimensional Navier-Stokes Calculations 上へ：Types of analysis 前へ：Hydraulic Networks 目次へ


開水路での乱流

開水路での乱流は1次元ネットワーク計算で近似することが可能です。理論的な背景については[16]、また特に[11]（オランダ語）を参照してください。支配方程式は Bresse の式で、これはベルヌーイの式の特殊例です。

図119: 開水路の形状
\begin{figure}\epsfig{file=channelsection.eps,width=12cm}\end{figure}

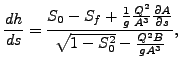$\displaystyle \frac{dh}{ds}=\frac{S_0 - S_f + \frac{1}{g} \frac{Q^2}{A^3} \frac {\partial A}{\partial s}}{\sqrt{1 - S_0^2} - \frac{Q^2 B}{g A^3}},$ (255)

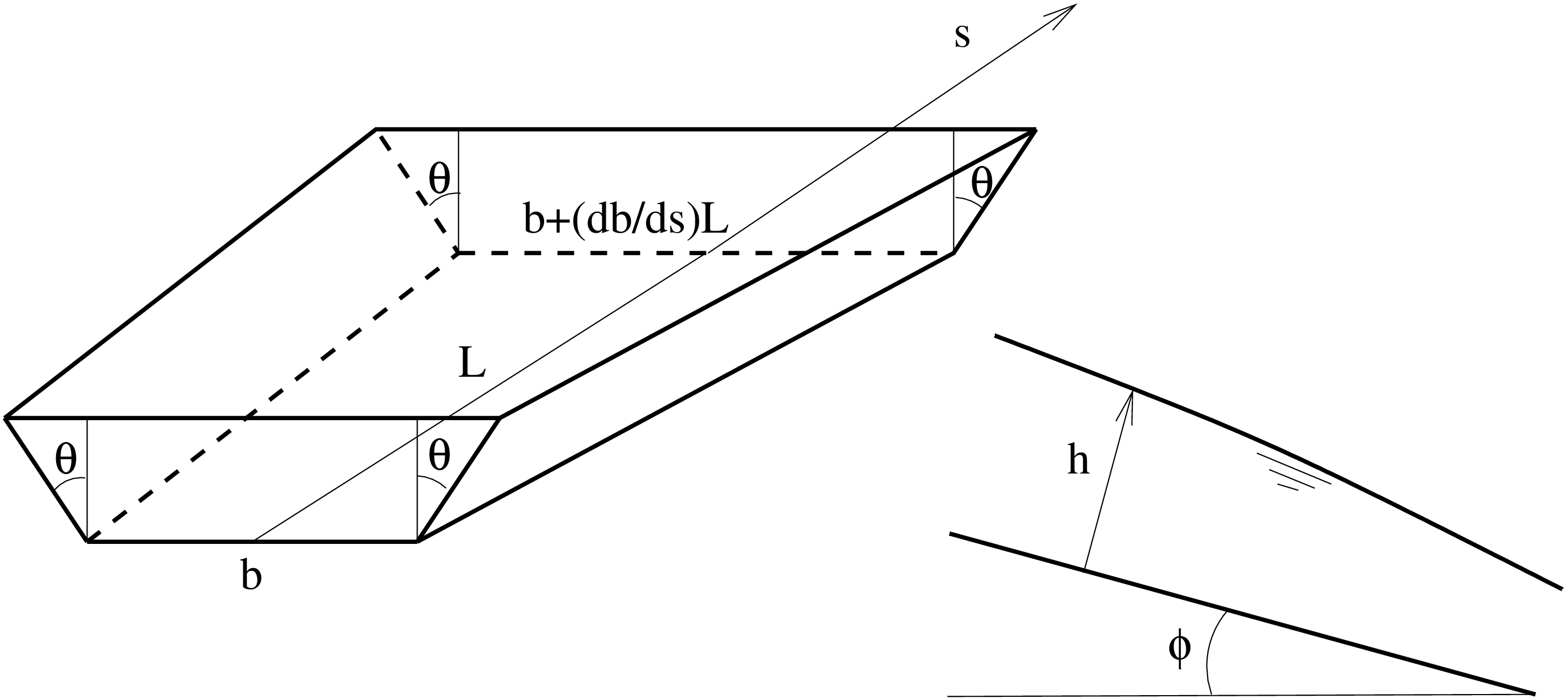
ここ（図119）で h は（開水路底面から垂直に測った）水深、s は底部沿った長さ、S0 = sin(φ)で φ は開水路と水平線のなす角、Sf は摩擦項、g は重力加速度、q は体積流量（質量流量を流体密度で割った値）、A は断面積、$ \frac {\partial A}{\partial s}$は h を固定した場合の s に対する断面積の変化、$ B$は水面での開水路の幅です。Bresse の式の導出では以下のような仮定がおかれます。

  1. 定常流れ
  2. 各断面は静水
  3. 各断面で流速は一定
  4. 各断面に対して流速ベクトルは垂直

Sf に関しては複数の式が提案されていますが、CalculiX では White-Colebrook 式と Manning 式が実装されています。White-Colebrook 式は以下の様な形をしています。

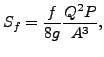$\displaystyle S_f=\frac{f}{8g} \frac{Q^2 P}{A^3},$ (256)

ここで f は式28によって決定される摩擦係数、P は断面の接液周です。一方、Manning 式は以下の様になります。

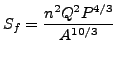$\displaystyle S_f=\frac{n^2 Q^2 P^{4/3}}{A^{10/3}}$ (257)

ここで n は Manning 係数で、これは実験的に決定されます。

CalculiX では開水路の断面は台形である必要があります（図119）。この形状の場合には以下の関係が成り立ちます。

$\displaystyle A=h(b+h \tan\theta),$ (258)

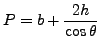$\displaystyle P=b+\frac{2h}{\cos\theta}$ (259)

$\displaystyle B=b+2h \tan\theta.$ (260)

要素内では底面幅 b は線形に変化させることができますが、他のパラメーターは全て変更できません。以上から次のような結果が得られます。

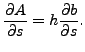$\displaystyle \frac{\partial A}{\partial s} = h \frac{\partial b}{\partial s}.$ (261)

1次元開水路ネットワークのために CalculiX で使用されている要素は標準的なネットワーク要素で、要素の未知数は端節点での液体深さ、温度と中間節点での質量流量です。使用できる方程式は中間節点での Bresse の式（運動量保存式）、端節点での質量とエネルギーの保存式（それぞれ式249、式253）です。

開水路流れは超臨界状態も未臨界状態も両方扱えます。超臨界流れでは流速は波の伝播測度 c を超え、$ c=\sqrt{gh}$を満たします。流体の速度を U としてフルード数を Fr = U/c と定義すると、超臨界流れは Fr>1 に対応します。超臨界流れは上流側の境界条件によって制御されます。流れが未臨界（Fr<1）の場合には、流れは下流側の境界条件によって制御されます。未臨界流れでは乱れは上流と下流の両方に伝播しますが、超臨界流れでは下流側にのみ伝播します。超臨界から未臨界への流れの遷移は跳水と呼ばれ、未臨界から超臨界への流れの遷移は滝になります。跳水位置では以下の式が満たされます[16]（運動量保存）。

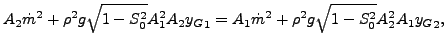$\displaystyle A_2 \dot{m}^2 + \rho^2 g \sqrt{1 - S_0^2} A_1^2 A_2 {y_G}_1 = A_1 \dot{m}^2 + \rho^2 g \sqrt{1 - S_0^2} A_2^2 A_1 {y_G}_2,$ (262)

ここで A1、A2 は跳水前後の断面積、yG1 と yG2 はそれら断面の重心、ρ は流体密度、$ \dot{m}$は質量流量です。滝が発生するのは開水路形状が不連続な位置、つまり非連続な開水路底面傾斜 S0 が不連続に増加する位置です。利用可能な境界条件は水門、堰、無限サイズのタンクです。これらはセクション6.6で説明されています。

出力変数は質量流量（*NODE PRINT カードまたは*NODE FILEカードのMFキー）、水深（*NODE PRINT カードのPNキー……Network Pressure…… と*NODE FILE カードのDEPTキー）、全温度（*NODE PRINT カードのNTキー、*NODE FILE カードのTTキー）です。これら変数はネットワークにおける主要変数です。内部的には、ネットワーク節点では変位場の第1成分から第3成分がそれぞれ質量流量、水深、臨界深度に使用されています。従って *NODE PRINT カードで U を使用しても出力を行なうことが可能です。.datファイルで臨界深度を取得する場合はこれが唯一の方法になります。.frdファイルでは *NODE FILE カードのHCRIを選択することで臨界深度を取得することができます。流体では全温度は実質的に静温度と一致することに注意してください（前セクションを参照。水深 1m の開水路での波の速度は$ \sqrt{10}$ m/s であることを思い出してください）。ネットワーク内で跳水が起きた場合、跳水が起きた場所の要素一覧と要素内での相対位置が画面上に表示されます。

次へ 上へ 前へ 目次へ
次へ：Three-dimensional Navier-Stokes Calculations 上へ：Types of analysis 前へ：Hydraulic Networks 目次へ
guido dhondt 2016-03-08