次へ 上へ 前へ 目次へ
次へ：Möhring 上へ：Fluid Section Types: Gases 前へ：Cross, Split 目次へ

渦

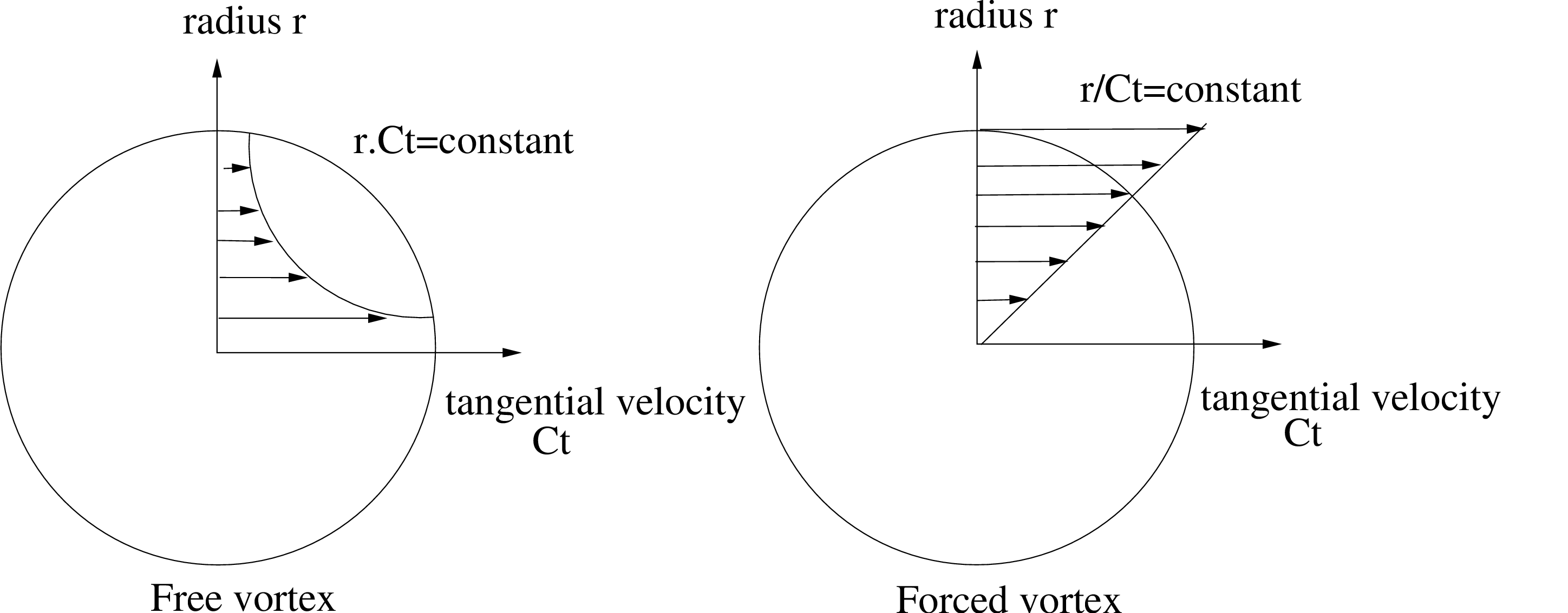
気体が回転機器に沿って流れる際には渦が生じます。気体の勢いが弱く、機器が高速に回転している場合には機器の回転エネルギーの一部が気体へ移動します。これを強制渦と呼びます。図92に見られるように半径の値が増えるにしたがって接線方向流速が増加するのが強制渦の特徴です。

図 92: 強制渦と自由渦
\begin{figure}\epsfig{file=definition_vortex.eps,width=12cm}\end{figure}

与えられた半径で実際の渦を持ち、軸を離れるに従ってその渦が消えるという気体もあり得ます。これは自由渦と呼ばれ、図92に見られるように接線流速が双曲的に減少するのが特徴です。初期渦は通常は先行する回転機器によって与えられるのが普通です。

図 93: 強制渦の形状
\begin{figure}\epsfig{file=forced_vortex.eps,width=10cm}\end{figure}

図93に示す通り強制渦はその上流側半径と下流側半径によっての形状的に特徴づけられます。流れの向きは中心に向かう向き、または中心から離れていく向きのどちらかで要素定式化はどちらでも動作します。0から1の間の値を取るコア・スワール比 Kr は回転機器によって気体がどれだけ回転するのかを表します。Kr=0 の場合には回転エネルギーの移動は起こらず、Kr=1 の場合には気体は機器と一緒に回転します。強制渦横断面での理論的な圧力比は以下を満たします。

$\displaystyle \left (\frac{p_o}{p_i} \right) _{theoretical}= \left[ 1 + \frac... ... (\frac{R_o}{R_i} \right) ^2 -1 \right) \right ] ^ {\frac{\kappa}{\kappa-1}},$ (22)

ここで添え字「i」は内部（最小半径）、「o」は外部（最大半径）、pは全圧、Tは全温度、Uは回転機器の接線速度をそれぞれ表します。この式は気体の接線速度が半径に対して線形に変化する（図92）という観測事実に基づいて立てられています。どの向きの流れであっても外側半径での圧力は常に内側半径での圧力より大きいということに注意してください。

圧力補正係数 η を使用することで渦横断面での理論的な圧力降下を補正することができます。圧力補正係数は以下で定義されます。

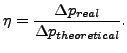$\displaystyle \eta=\frac{\Delta p_{real}}{\Delta p_{theoretical}}.$ (23)

最後にパラメーター Tflag によって渦による温度上昇を制御することができます。原則的には気体へ移動する回転エネルギーは同時に温度の上昇をもたらします。もしその効果を計算に含めたくなければ Tflag=0 を選択する必要があります。それ以外の場合は渦が絶対座標で定義されているか、回転機器に固定された相対座標で定義されているかどうかに従ってそれぞれ Tflag=1 または Tflag=-1 を指定してください。渦要素が絶対・相対気体要素に先行され、相対・絶対気体要素が後に続くネットワーク内の点に設定されている場合には相対座標系が有効化されます。計算される温度上昇は Kr=1 でだけ補正されます。まとめると強制渦要素は以下の定数で表されます（*FLUID SECTION, TYPE=VORTEX FORCED カードの下の行で順に指定されます）：

自由渦では流入口での気体の接線流速 Ct の値が最も重要なパラメーターになります。この値は先行する要素の数 n を指定することで定義されます。先行する要素は通常はプリスワール・ノズルか別の渦で、接線流速を与えます。この場合には値 N は使用されません。遠心流れでは与えられた接線流速 Utheorical をスワール損失係数 K1 で大幅に変更することが可能です。スワール損失係数は以下で定義されます。

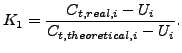$\displaystyle K_1=\frac{C_{t,real,i}-U_{i}}{C_{t,theoretical,i}-U_{i}}.$ (24)

また n=0 が指定された場合、流入口での接線流速には気体に旋回させる機器の回転速度 N が使用されます。この場合には K1 と U1 は使用されません。自由渦横断面での理論的な圧力比は以下を満たします。

$\displaystyle \left (\frac{p_o}{p_i} \right) _{theoretical}= \left[ 1 + \frac... ...eft (\frac{R_i}{R_o} \right) ^2 \right) \right ] ^ {\frac{\kappa}{\kappa-1}},$ (25)

ここで添え字「i」は内部（最小半径）、「o」は外部（最大半径）、「up」は上流側、pは全圧、Tは全温度、Ctは気体の接線速度をそれぞれ表します。この式は気体の接線速度が半径に対して反比例して変化する（図92）という観測事実に基づいて立てられています。どの向きの流れであっても外側半径での圧力は常に内側半径での圧力より大きいということに注意してください。

ここでも圧力を圧力補正係数 η によって補正することができます。また温度変化を考慮するかどうか決めるためのパラメーター Tflag が用意されています。ただし自由渦では絶対座標系の場合には温度が変化しないことに注意してください。まとめると自由渦要素は以下の定数で表されます（*FLUID SECTION, TYPE=VORTEX FREE カードの下の行で順に指定されます）：


サンプルファイル: vortex1、vortex2、vortex3

次へ 上へ 前へ 目次へ
次へ：Möhring 上へ：Fluid Section Types: Gases 前へ：Cross, Split 目次へ
guido dhondt 2016-03-08