序論

1. 機械使用の目的

機械を使用する目的は所要の運動を得る為か、もしくは力を変化する為なり。機械は動力を創造する事能わずして単に動力の状態を変化するものなり。例えば小なる力を大なる力に換えんとするが如き、不規則の運動を整然たる運動又は特種の運動に化せんとするが如き、遅き運動を速き運動に化せんとするが如き、あるいはその逆の如き、自然エネルギーを機械的動力に換えるが如し。

2. 機械の定義、及びその特性

機械は抵抗性ある物体の組合にしてその各の組子の関係的運動はまったく限定せられ、之によって与えられたるエネルギーを所要の特種の仕事に変ぜしむるものなり。

以上の定義により機械は次の特性を有す：

1. 二個もしくは二個以上の物体の組合。

   組み合わせたる物体の各を組子と称す。各組子は次の如く大別し得：

   1. エネルギーを受け入るる組子。
   2. 機械的動力を伝達するかあるいは特種の動力に変更する組子。
   3. 所要の仕事を為す組子。
   4. 静止状態にありて以上の 1, 2, 3 の全ての組子を支える組子。之を架構、あるいは枠と称す。

2. 組子は抵抗性を有す。

   組子は受くる力によりて歪みを生ずるも使用に支障を生ぜず。又その材料は受くる力に対して充分安全なる程度なるを要す。之を抵抗性と称す。鉄性もしくは木製リンクは引張にも収縮にも抵抗して機械の組子を為す。ベルトもしくは綱等は引張を受くるときのみ抵抗性ありて機械の組子となる。ポンプもしくは水圧機の水は圧縮に対する抵抗性ありて機械の組子を為す。

3. 各組子は限定運動を為す。

   各組子の運動はその受くる力の大小、及び方向の如何に拘らず規定の運動を為す即ち限定運動を為す。故に各組子の運動の路は一定なり。一般に物体が自由の状態にあるときは力の加わる方向に動くか、あるいは物体が既にある方向にある速度にて運動しつつあるときは更にその受くる力の方向に分速度を生じ、之が在来の速度と合成して在来とは異なれる方向に合成速度を以て運動し始むるものとす。然るに機械においては各組子の運動の路は予め定まり組子に加わる力は力の方向の如何に拘らず組子が動く方向に分力として加えらる。即ち加えられたる力の一分力が組子に加わりて運動を生じ他の直角の分力は摩擦的作業を為す。されば後者の大なるほど機械の有効仕事量減ず。されば機械に与えられたるエネルギーは実際にはその一部分有効仕事を為し、残りの部分が無効仕事を為す。即ち、

    供給されたるエネルギー＝有効仕事＋無効仕事

   有効仕事と供給されたるエネルギーとの比をその機械の効率と称す。一般に効率は百分率 ％ にて表わす。無効仕事は摩擦無効仕事又は衝撃等にして多くは熱又は音となりて消散し、復た収容すべからず。

   完全機械とは供給されたるエネルギーの全部を要求せる仕事に変ずる機械の謂いにしてその効率は 100％ なり。

   機械の組子が速度を増す場合には供給されたるエネルギーの幾分が運動のエネルギーに変更すれども速度の減ずるに従いエネルギーを吐出す。ハズミ車（勢車）の回転の如き、ピストン、連棹等の運動の如き、その例なり。

4. エネルギーを特種の仕事に変ず。

   抵抗に逆らって物体を動かすを仕事を為すと言う。仕事量は物体が動きたる距離とその動く方向に逆いたる抵抗力との相乗積にて表わし得。されば P キログラムの抵抗に逆らって力の方向に全く反対に物体を L メートル動かしたるときは PL キログラムメートルの仕事を為す。物体の動く方向が抵抗する力と常に角 θ を為すときは PLcosθ キログラムメートルの仕事を為す。原動機の出力又は機械を運転するに要する動力を計るに単位時間における一定仕事量を単位とす。通常は単位として馬力を用う。一馬力とは毎秒 75 キログラムメートルの仕事を為す割合なり。例えば 150 キログラムの張力に対して毎秒 3 メートル曳く仕事は毎秒 450 キログラムメートルの仕事の割合にして 6 馬力なり（フィート、ポンドの英国単位にて表わせば一馬力は毎分 33,000 フィートポンドの仕事を為す割合なり）。完全機械において一組子の動く方向に P キログラムの力を加えて a メートル動かし之によって他の組子を抵抗 Q キログラムに逆らってその方向に b メートル動かしたるときは Pa キログラムメートルのエネルギーを機械に加えて Qb キログラムメートルの仕事を為すが故に Pa=Qb、即ち Q:P=a:b。Q/P を力比、b/a を連比と言う。故に完全機械にありては 連比×力比=1。即ち連比大なれば力比は小に、連比小なれば力比大なり。換言すれば「力に益あれば動く距離に損あり」。力比を機械の利益と言う。

   仕事に変すべき自然エネルギーは

   1. 人間その他の動物の筋力によるエネルギー
   2. 風のエネルギー
   3. 水のエネルギー
   4. 水蒸気、空気、その他のガス体に加わりて膨張仕事を為す熱
   5. 電気等

   なり。2 ないし 4 のエネルギーは何れも原動機によりて回転運動を為す機械的動力に変更せらる。

   風車、水車、蒸気機関、ガスエンジン、石油エンジン等の原動機はそれぞれ風、水、水蒸気のエネルギー、ガス又は石油の爆発エネルギーを機械的動力に変更す。紡績錘車の車軸は多大の力を要せざれど非常に高速に回転するを要し、之を直接手にて回転せしむる事能わず。然れども紡績錘車の機械仕掛は大車を緩慢に回転して良く目的を達し得。裁縫機の針の上下運動は吾人如何に熟達するも直接に彼の如く急速に運動せしむる事能わず。テコは吾等の筋力にて直接に動かし得ざる荷物を動かし、不規則なる回転力にてバネを巻き之に貯えたるエネルギーを、時計は良く長針、短針の等速運動として吐出す。

   上述の自然エネルギーを第一次エネルギーと称し原動機によりて生ずる回転運動エネルギーを第二次エネルギーと称す。諸製造及び工作機械は第二次エネルギーによりて運動せらる。

   機械作業に二大要素あり。力及び運動とす。ある機械は力を主とし力を増大するを目的とし、ある機械は運動を主とし特殊運動を為すを目的とす。

3. 機構の定義

二個もしくは二個以上の組子の組合にしてその一つの組子に対して他の組子が限定運動を為すものを機構と称す。

機構において之を構成する任意の一つの組子が静止の組子と為り得。之が為めにある一機構が限定運動の状態全く異なる別の機構を生む。之を機構の転置と称す。

4. 機構のツガイ

機構を構成する組子の組合の最も簡単なるは二個の組子の組合にして之をツガイと称す。ツガイは二個の組子が面を以て接触するのと線又は点を以て接触するものとの二種あり。前者を面ツガイ（低次対）と称し。後者を微面ツガイ（高次対）と称す。面ツガイには次の四種あり：

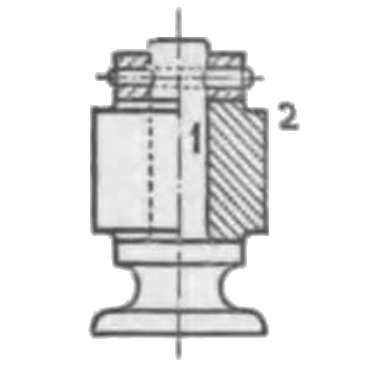
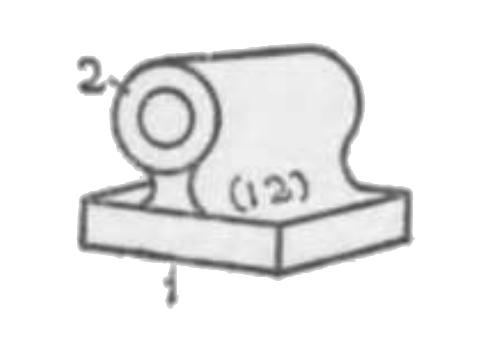
1. 回りツガイ。第一図の如きその一例にしてその 1, 2 何れかの組子を静止するときは他の組子はその軸を軸として回転しその他の運動をなさず。
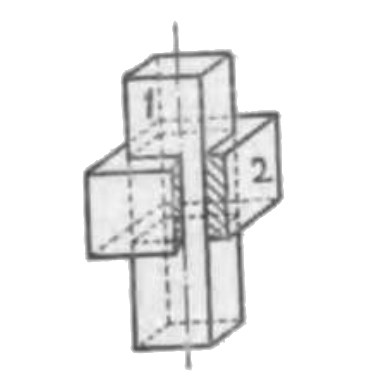
2. 滑りツガイ。第二図の如きその一例にしてその 1, 2 何れかの組子を静止するときは他の組子は直線運動を為す。この運動方向は軸に平行す。
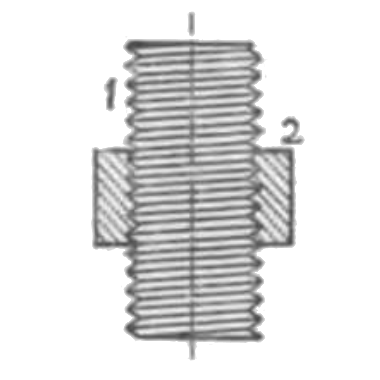
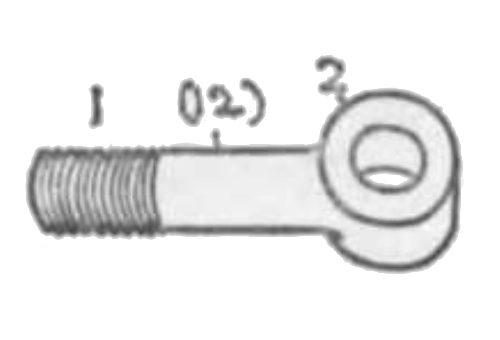
3. ネジツガイ。第三図の如きその一例にしてその 1, 2 何れかの組子を静止するときは他の組子は回転しつつ、かつ軸方向に直線運動を為す。
4. 球ツガイ。第四図の如きその一例にして 1, 2 は球面を以て接触す。その何れかの組子を静止するときは他の組子はこの球の中心を中心とする球運動を為す。

5. 機械的運動

機構によりて仕遂げらるる運動を機械的運動と称す。機械的運動は限定運動にして次の如き種類あり。

第一種：

1. 連続運動　運動する点の路が閉曲線を為す運動なり。
2. 往復運動　運動する点が一定の路を進み次にその路を逆行する運動を往復運動と称す。時計の振子において見るが如き往復円弧運動を特に揺動と言う。
3. 途切れ運動　運動中に静止ある運動を途切れ運動と称す。

第二種：

1. 平面運動　運動する物体の各点がそれぞれ与えられたる一平面に並行に運動するを平面運動と称す。
2. 螺旋運動　運動する物体の各点が一軸の周囲に回転しつつ同時にその軸に並行に運動するを螺旋運動と称す。通常、回転角速度と軸方向の線速度との比一定なり。
3. 球面運動　運動する物体の各点が一つの定まれる点より距離を変ずる事なくして運動するを球面運動と称す。

サイクル　機械の各の組子は一定の運動を為さば再び前述の運動を繰り返して行い、斯くして循環的に運動を為す。この運動の一循環をサイクルと称す。一サイクルの運動に要する時間を周期と称す。

相　機械の各組子の運動の瞬時状態を相と称す。

6. 運動伝達の方式

動者、被動者、中継　機構においてはその一組子を動かせば他の組子もまた動く。前者を動者、後者を被動者と称す。機構が数多の組子より構成せられ、その一つが動者となり順次に他の組子を動かし遂に最後の被動者を動かす機構を機構のツナガリと称す。動者と被動者との中間組子を中継と称す。

機構において動者が被動者に動力を伝達するに次の方式あり：

1. 直接接触による。
2. 中継接続による。

歯車又はカムの如きは動者が被動者に直接接触によりて動力を伝える例なり。中継には次の三種あり。機関のクロスヘッドの往復直線運動をクランクの回転運動に変ずる連桿の如きは剛体中継、二つの調車に掛けられたるベルトの如きは纏捲中継、ポンプの水筒中の水の如きは流体中継と称す。

二個、あるいは二個以上の機構が組合されて機械的運動を為すものを複式機構と称す。

一つの機構又は複式機構においては被動者の運動は一般に動者の運動と種類、速度、方向の三者を異にす。例えば等速回転運動を、（甲）急速なる等速回転運動に変ずるが如き、（乙）途切れ運動に変ずるが如き、（丙）指定の方向に甚だ遅き速度にて被動者を動かすが如し。

7. 平面機構と立体機構

機構の各組子の運動が与えられたる一平面に並行するものを平面機構と称し、然らざるものを立体機構と称す。機械の多数は平面機構より成る。

8. リンク

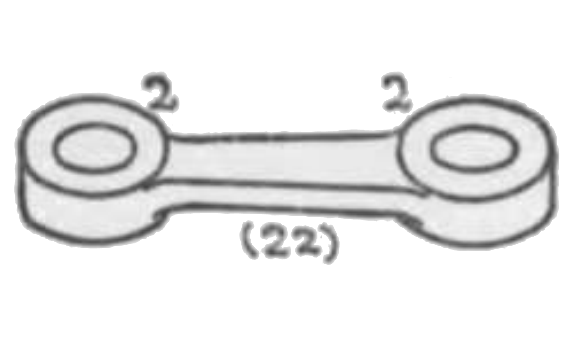
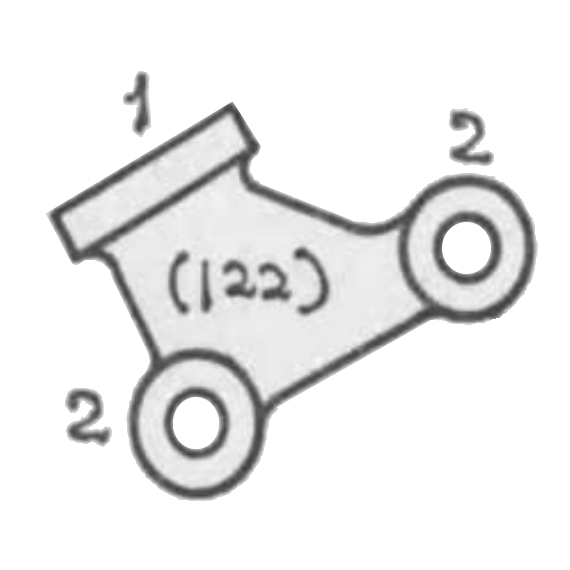
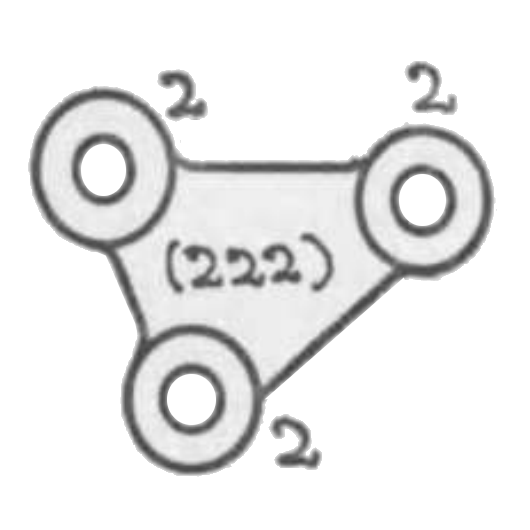
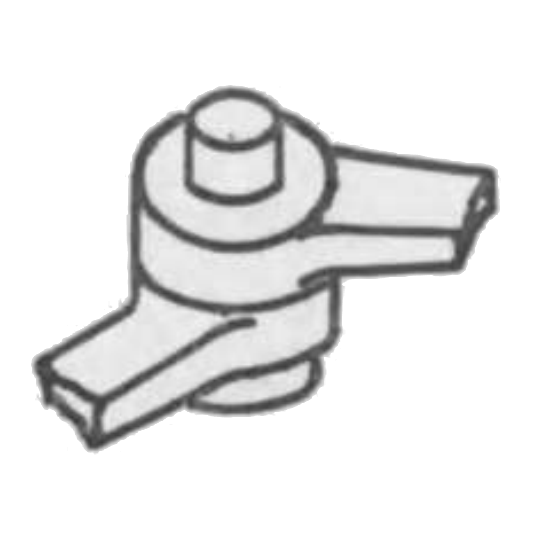
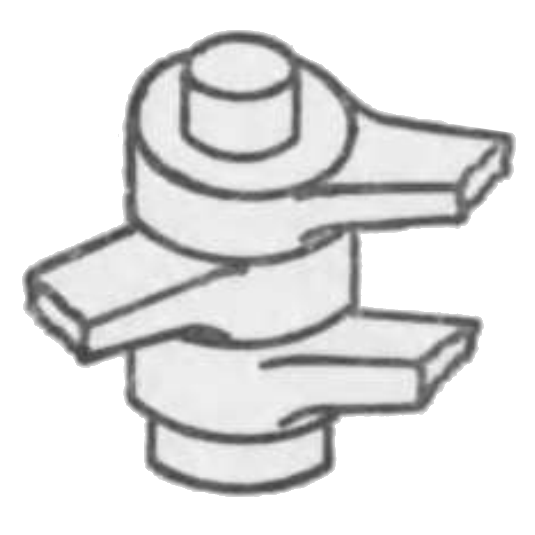
その軸を並行にせる二個の回りツガイの一組子 2, 2 を固体にて連結して一体とせしものをリンクと称するを普通とするが二あるいは二以上のツガイの何れか一個を固体にて連結して一体とせしものをリンクと称す。而して二組子を一体とせしものを二元リンクと称し三組子を一体とせしものを三元リンクと称す。第五、六、七図は何れも二元リンクにして第八、九図は何れも三元リンクの例なり。同様に四個の組子を一体とせしものは四元リンクなり。

9. 蝶ツガイ

二個の回りツガイがその軸を共通したる形、即ち第十図に示すものを蝶ツガイと称するを普通とするが之を二元蝶ツガイと称し三個の回りツガイが軸を共有したる形、即ち第十一図に示すものを三元蝶ツガイと称し斯くして四元蝶ツガイをも知り得。

註：

運動と静止

運動、静止は関係的の語なり。物体甲乙が関係的位置を変ずるときは乙は甲に対して運動しあるいは甲は乙に対して運動すと言う。 甲乙が関係的位置を変ぜざるときは乙は甲に対して静止しあるいは甲は乙に対して静止すと称す。甲を静止するとして他の物体の運動を論ずる場合は甲を運動の基標と称す。されば地上に建てる家屋又は運動せざる機械は地球を運動の基標とするときは静止す。然れども地球が太陽に対して運動を為すにより、以上の家屋又は機械は太陽を運動の基標とするときは運動す。汽車の客車内に安座する旅客は客車に対しては静止すれども地球（即ち地面）に対しては運動す。故に他物の存在を考えずして、即ち運動の基標なくして一物体の運動、静止を認定すること能わず。甲を運動の基標として乙が静止するとき乙を運動の基標とするときは甲は静止す。又甲に対して乙が運動するときは乙に対して甲は運動す。甲に対して乙の運動を知り又乙に対して丙の運動を知るときは甲に対して丙の運動を知り得（運動第二法則）。されば運動、静止は関係的にして甲を運動の基標としての乙の運動を甲に対する関係運動と言う。

運動の路、方向、速度

空間に連続運動する点は線を描く。之を路と称す。路には曲線、直線等種々あり。一物体が運動するときはその内の諸点あるいは之に属する諸点はいずれも路を描く。路より運動を知り得。一物体の運動はこれに属する三点の路にて決定し得。

時計に向って針の回転する方向を右回転と称し、之に反する方向の回転を左回転と称す。

運動する点の路が直線なるとき点の移動する方向が運動の方向にして点の移動する距離を移動に費やされたる時間にて除したる数をこの直線運動の平均速度と称す。運動の時間が甚だ微小にして移動の距離も従って短縮するときの平均速度は算定し得。而して運動の時間を無限小ならしむるときは点は甚だ接近する位置に移ることとなる。この場合の平均速度をその点の瞬間速度と称す。運動する点の路が曲線なれば運動せる点を接点とせる接線の方向がその接点の運動の方向なり。 瞬間速度とは運動する点がその点の位置より瞬時に次の位置に同一の状態にて運動を継続すると考えられたる場合の方向及び速度なり。

等速運動、等加速度運動

運動する点の路の各点における瞬間速度一定なるときは之を等速運動と称す。運動する点の瞬間速度が一様ならずして時の経過に正比例して増しあるいは減ずるときは之を等加速あるいは等減速運動と称す。車軸が回転する角度（単位はラジアン又は一度）を回転に費されるる時間にて除したる数をこの時間内の平均角速度と称す。前者の線速度の例に倣いて瞬間角速度等の術語の意味をも解し得。

• 度

  直角の九十等分の一を一度。 一度の六十等分の一を一分。一分の六十等分の一を秒と称す。而して五十七度十七分四十五秒は 57° 17′ 45′′ と記す。

• ラジアン

  円の半径に等しき長さの円弧の中心角にして 180 / π = 57.29578 約 57° 17′ 45′′

回転する軸の角速度は実用上単位時間の回転数にて表わす。例えば角速度を毎分六百、あるいは毎秒十にて言い表わすが如し。