 |
このセクションでは円筒形コンデンサーの静電容量を計算します。コンデンサーの内径は1m、外径は2m、長さ10mです。 コンデンサーは空気で満たされていて、その誘電率は ε0=8.8542×10-12 C2/Nm2です。テスト例パッケージのひとつである入力デッキの抜粋を以下に示します:
*NODE, NSET=Nall ... *ELEMENT, TYPE=C3D20, ELSET=Eall ... *NSET,NSET=Nin 1, 2, ... *NSET,NSET=Nout 57, 58, ... *SURFACE,NAME=S1,TYPE=ELEMENT 6,S3 1,S3 *MATERIAL,NAME=EL *CONDUCTIVITY 8.8541878176e-12 *SOLID SECTION,ELSET=Eall,MATERIAL=EL *STEP *HEAT TRANSFER,STEADY STATE *BOUNDARY Nin,11,11,2. Nout,11,11,1. *EL FILE HFL *FACE PRINT,SURFACE=S1 FLUX *END STEP
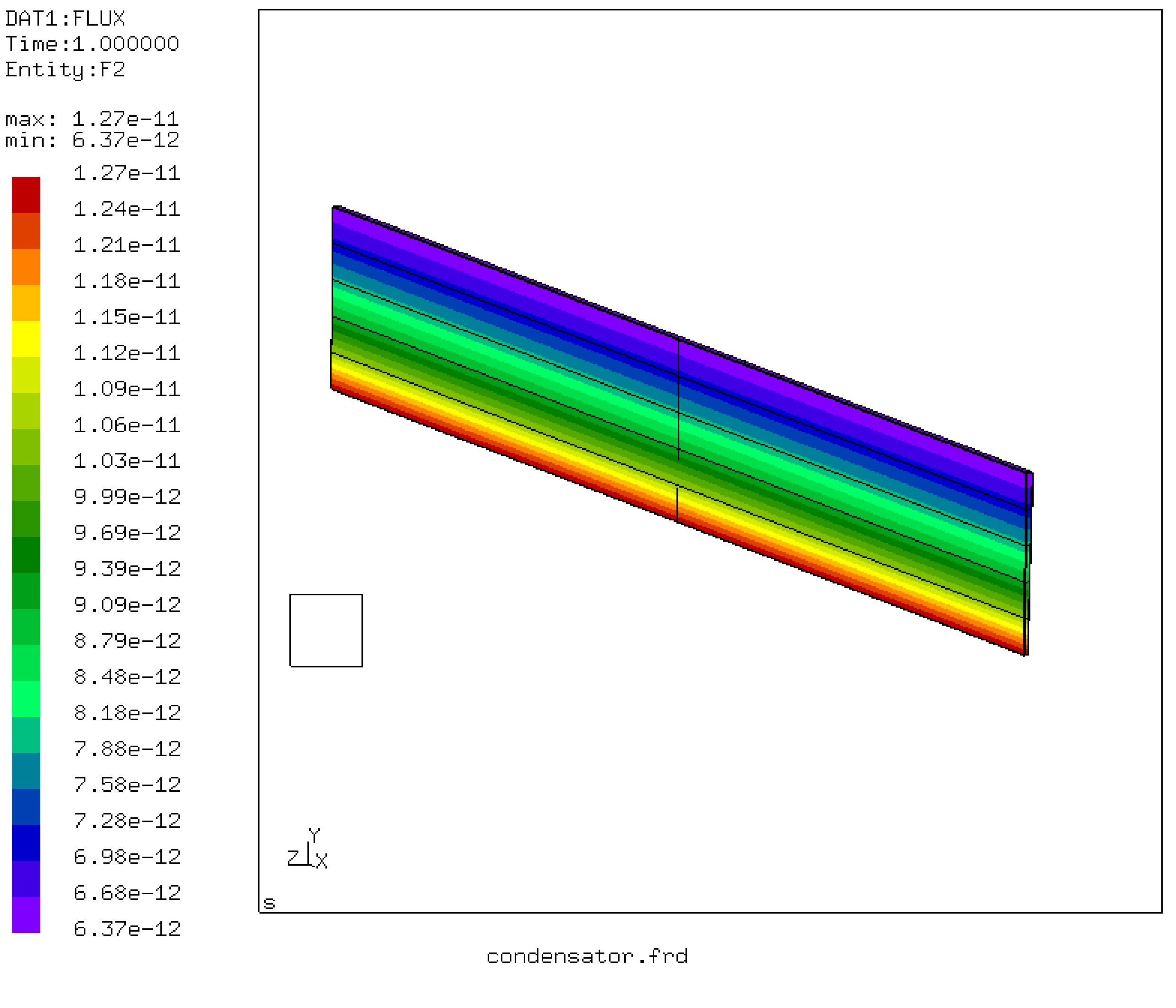
セクション6.9.13で説明されている通り、静電容量は、 電極板間の単位温度の差に従ってコンデンサーの電極板のひとつを通過する全熱フラックスを決定することで計算可能です。 コンデンサーの電極板の間の材質にはその誘電率と同じ伝導率が割り当てられます。ここではコンデンサーの中の1度分のみモデル化します。 軸方向のメッシュが非常に荒いのは、温度変動がないと想定しているためです。 図24から内径位置での熱フラックスが 1.27×10-11 W/m2であることがわかります。全熱フラックスに換算するとこれは 7.98-10 Wになります。コンデンサーの解析公式から 2πε0/ln(2)=8.0261-10 C/Vと求まります。
入力デッキの *FACE PRINT キーワードによって内側の電極板S1の全熱フラックスも.datファイルに出力されます。 そこでは -2.217×10-12 Wと見積もられています。 この値が負の値なのは流れがコンデンサーの電極板間の空間に流れ込んでいるためです。 モデル化されているのは1度分のみなので、この値には360を掛ける必要があり、360を掛けると上記と同じ値になります。