同次線形方程式

同次線形方程式は以下の形をとります。

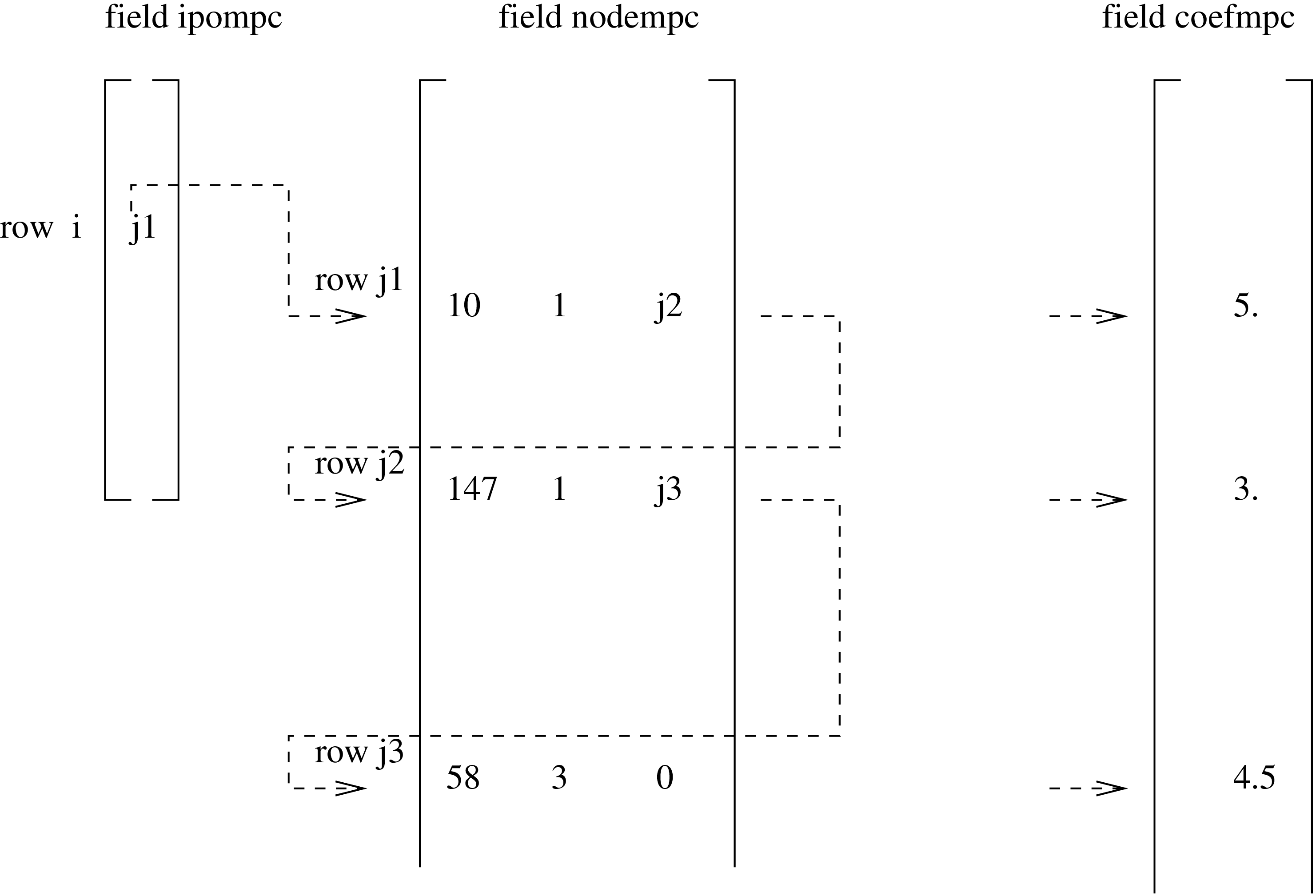
変数 n は任意の整数で、線形方程式は任意の個数の項を含むことができます。これら方程式（MPC とも呼ばれます）の保持には1次元フィールド ipompc と3つの列を持つ2次元フィールド nodempc が使用されます。MPC i ではフィールド ipompc の行 i にフィールド nodempc の行が格納され、そこから MPC i の定義が開始します。ipompc(i)=j であれば MPC の最初の項の自由度は節点 nodempc(j,1) の方向 nodempc(j,2) に対応します。この項の係数は coefmpc(j) に保存されています。nodempc(j,3) の値は MPC の次の項の情報を持つフィールド nodempc の行です。これが nodempc(k,3)=0 まで続きます。つまりフィールド nodempc の行 k の項が MPC i の最後の項です。

例えば以下の様な MPC を考えてみましょう。

ここで u₁(10) は節点番号 10 のグローバル X 方向の変位を意味します。他の項も同様です。この MPC が方程式番号 i であるとします。この時、この方程式は図136の様に格納されます。

図136: 線形方程式の保持のされ方の例

MPC の最初の項は中でも特別で、従属項と見なされます。有限要素計算ではこの様な従属項に対応する自由度は他の項の関数として書き下され、方程式系から取り除かれます。従って従属項の自由度には他の制約は課されません。MPC の従属項の自由度は SPC の場合と同様に分類されます。この目的のために1次元フィールド ikmpc に従属自由度が順番に格納され、1次元フィールド ilmpc には対応する MPC 番号が格納されます。これらフィールドの意味は ikboun と ilboun と完璧に対になっているので詳細については前のセクションを参照してください。

さらに MPC にはラベルが付けられています。MPC i のラベルは labmpc(i) に保存されます。これは1次元のフィールドで、1要素は長さ20の文字列（FORTRAでの character*20）からなります。ラベルは MPC の種類を表します。現在のところ、以下の種類が使用されています。

• CYCLIC: 周期対称拘束を意味します
• MEANROT: 平均回転拘束を意味します
• PLANE: 平面拘束を意味します
• PRETENSION: 事前張力条件を表す事前張力 SPC
• RIGID: 剛体拘束を意味します
• STRAIGHT: 直線拘束を意味します
• SUBCYCLIC: 項のいくつかが周期対称拘束の一部である線形 MPC を意味します。
• THERMALPRET: 事前張力セクションで新しく作成された節点での熱境界条件。純粋な機械計算で必要になります。

MEANROT MPC、PLANE MPC、STRAIGHT MPC は *MPC キーワード・カードで、RIGID MPC は *RIGID BODY キーワード・カードで、CYCLIC MPC は *CYCLIC SYMMETRY MODEL カードで設定します。SUBCYCLIC MPC はユーザーが明示的に有効化することはできず、プログラムで内部的に設定されます。

非同次の MPC は新しい自由度を導入し、SPC を使って非同次項をその項に割り当てることで同次化することが可能であることに注意してください。非線形 MPC は線形化を施すことで線形 MPC へ変形可能です[18]。CalculiX では現在のところ PLANE MPC、STRAIGHT MPC、USER MPC、RIGID BODY 定義でこれが行なわれています。ローカル座標系の SPC は線形 MPC へ変換されることに注意してください。

最後に、変数 icascade についてです。この変数は MPC が最新のイテレーションから変わったかどうかを調べるためのものです。これは非線形 MPC が適用された場合（例. 係数の1つがある時はゼロで、別の時は非ゼロ）、または接触条件の下にある場合に起きることがあります。この機能はまだ対応されていません。今のところは icascade はゼロ、つまり MPC がイテレーション間で変わることはないと仮定されています。