次へ
上へ
前へ
目次へ
次へ:Loading
上へ:Theory
前へ:Electromagnetism
目次へ
指定されたインクリメント終了時での解を見つけるためには一連の非線形方程式を解かなければいけません。これを行なうためにニュートン・ラフソン法が使用されます。つまり一連の方程式は局所線形化されて解かれるのです。解が元の非線形方程式を満たさない場合には新しい解で再度線形化が行なわれます。ある限度内で解が元の非線形方程式を満たすまで、この処理は繰り返されます。イテレーション i ごとに収束したかどうかがチェックされます。ここで以下のような量を導入してみましょう。
-
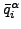 :イテレーション i が終わった時点での場 α の平均フラックス。これは以下の様に定義されます。
:イテレーション i が終わった時点での場 α の平均フラックス。これは以下の様に定義されます。
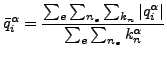 |
(322) |
ここで e は全要素の代表、ne は指定された要素に属する全ての節点、kn は指定された節点に属する場 α の全自由度であり、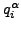 はイテレーション i 終了時の指定された要素・節点での指定された自由度のフラックスを意味します。今のところ、CalculiX には2種類のフラックスがあります。力学計算での力と熱計算での集中熱フラックスです。
はイテレーション i 終了時の指定された要素・節点での指定された自由度のフラックスを意味します。今のところ、CalculiX には2種類のフラックスがあります。力学計算での力と熱計算での集中熱フラックスです。
-
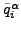 :現在のインクリメントの全イテレーション(ただしイテレーション i を含まない)での場 α のイテレーション平均フラックス
:現在のインクリメントの全イテレーション(ただしイテレーション i を含まない)での場 α のイテレーション平均フラックス
-
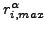 :イテレーション i 終了時の場 α の最大残差フラックス(絶対値)。各自由度は互いに独立であるとして計算されます。
:イテレーション i 終了時の場 α の最大残差フラックス(絶対値)。各自由度は互いに独立であるとして計算されます。
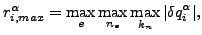 |
(323) |
ここで δ はイテレーション i による変化量を意味します。
-
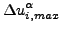 :イテレーション i を含む現在のインクリメントでの場 α の最大変化量(絶対値)
:イテレーション i を含む現在のインクリメントでの場 α の最大変化量(絶対値)
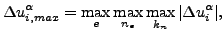 |
(324) |
ここで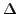 は現在のインクリメントによる変化量を意味します。力学計算では解は変位、熱計算では解は温度です。
は現在のインクリメントによる変化量を意味します。力学計算では解は変位、熱計算では解は温度です。
-
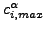 :イテレーション i での場 α の解の最大変化量(絶対値)
:イテレーション i での場 α の解の最大変化量(絶対値)
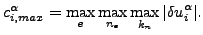 |
(325) |
ここで2つの定数 c1 と c2 が登場します。c1 はフラックスの収束をチェックするために使用され、c2 は解の収束をチェックするために使用されます。これらの値はゼロフラックス条件が有効かどうかによって変わります。ゼロフラックスは以下の様に定義されます。
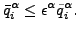 |
(326) |
ここで以下のルールが適用されます。
- if(
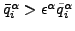 )(ゼロフラックスなし)
)(ゼロフラックスなし)
- else(ゼロフラックス)
![$ c_1=\epsilon^\alpha [{10}^{-5}]$](img1187.png) ,
, ![$ c_2=C_\epsilon^\alpha [0.001]$](img1188.png)
四角かっこの中の値はデフォルト値です。これらの値は*CONTROLSキーワード・カードを使用して変更することができます。収束と判定されるのは
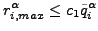 |
(327) |
かつ、熱・熱力学計算(*HEAT TRANSFER、*COUPLED TEMPERATURE-DISPLACEMENTまたは*UNCOUPLED TEMPERATURE-DISPLACEMENT)では温度変化が DELTMX を超えず、
なおかつ、以下の条件のうちの少なくともひとつが満たされる場合です。
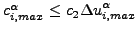
-
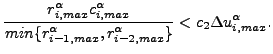 |
(328) |
左辺は次のイテレーションでの解の最大補正の推定値です。この条件は気体温度が計算されない場合(強制対流無し)のみ使用されます。
-
![$ r^{\alpha}_{i,max} \le R_l^\alpha [10^{-8}] \tilde{q}^{\alpha}_i$](img1192.png) 。この条件が満たされている場合、インクリメントは線形で、解の収束チェックは行なわれません。この条件は気体温度が計算されない場合(強制対流無し)のみ使用されます。
。この条件が満たされている場合、インクリメントは線形で、解の収束チェックは行なわれません。この条件は気体温度が計算されない場合(強制対流無し)のみ使用されます。
-
![$ \bar{q}^{\alpha}_i \le \epsilon^\alpha [10^{-5}] \tilde{q}^{\alpha}_i$](img1193.png) (ゼロフラックス条件)。この条件は気体温度が計算されない場合(強制対流無し)のみ使用されます。
(ゼロフラックス条件)。この条件は気体温度が計算されない場合(強制対流無し)のみ使用されます。
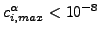
収束に到達し、またインクリメントのサイズがユーザーによって固定されていない(*STATIC カード、*DYNAMIC カード、*HEAT TRANSFER カードで DIRECT パラメーターが設定されていない)場合、特定の条件下では次のインクリメントのサイズが変更されます。
-
i > IL[10] の場合、dθ = dθDB[0.75]。ここで dθ はステップのサイズに対する相対的なインクリメントのサイズです(収束が極端に遅い場合にはインクリメントのサイズが減少)。
-
i ≤ IG[4] かつ前のインクリメントと同じサイズが適用される場合には dθ = dθDD[1.5] となります(収束が速いのでインクリメントのサイズが増加)。
イテレーション i で収束に到達しない場合、以下の処理が行なわれます。
次へ
上へ
前へ
目次へ
次へ:Loading
上へ:Theory
前へ:Electromagnetism
目次へ
guido dhondt
2016-03-08
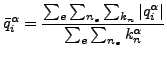
![]() はイテレーション i 終了時の指定された要素・節点での指定された自由度のフラックスを意味します。今のところ、CalculiX には2種類のフラックスがあります。力学計算での力と熱計算での集中熱フラックスです。
はイテレーション i 終了時の指定された要素・節点での指定された自由度のフラックスを意味します。今のところ、CalculiX には2種類のフラックスがあります。力学計算での力と熱計算での集中熱フラックスです。
![]() は現在のインクリメントによる変化量を意味します。力学計算では解は変位、熱計算では解は温度です。
は現在のインクリメントによる変化量を意味します。力学計算では解は変位、熱計算では解は温度です。
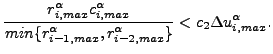
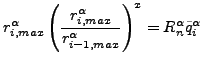
![$\displaystyle i+\frac{\ln \left(R_n^\alpha \frac{\tilde{q}^{\alpha}_i}{r^{\alp...
...\ln \left(\frac{r^{\alpha}_{i,max}}{r^{\alpha}_{i-1,max}} \right) } > I_C [16]$](img1211.png)