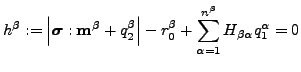Cailletaud の単結晶モデル

Georges Cailletaud らの単結晶モデル[49][50]は単結晶を作る金属成分の微小粘塑性を記述したものです。すべり面の向きと面内でのすべり方向は広く知られていて、それぞれ法線ベクトル n^β と方向ベクトル l^β で記述されます。ここで β はすべり面／すべり方向の組み合わせのひとつを意味します。すべり面とすべり方向は、以下を満足するすべり向きテンソル m^β を使って書き直すことができます。

m^β = (n^β ⊗ l^β + l^β ⊗ n^β)/2

(162)

全ひずみは弾性ひずみと塑性ひずみの合計と考えることができます。

各すべり面で、降伏曲面の等方的・動的変化を表すために等方硬化の変数 q₁ と移動硬化の変数 q₂ を導入します。この時、向き β の降伏曲面は以下の様になります。

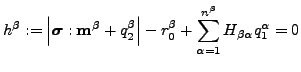$\displaystyle h^\beta := \left\vert \mbox{\boldmath${\sigma}$} : \mathbf{m^\bet... ...ght\vert - r_0^\beta + \sum_{\alpha=1}^{n^\beta} H_{\beta\alpha} q_1^\alpha = 0$

(164)

ここで n^β は考えている材料のすべりの向きの数、σ は応力テンソル、 $r_0^\beta$ はゼロ降伏での弾性範囲サイズ、H_βα は相互作用係数の行列です。硬化変数の構成方程式は以下を満たします。

$\displaystyle q_1^\beta = -b^\beta Q^\beta \alpha_1^\beta$

(165)

$\displaystyle q_2^\beta = -c^\beta \alpha_2^\beta$

(166)

ここで $\alpha_1^\beta$ と $\alpha_2^\beta$ はひずみ空間内の硬化変数です。応力の構成方程式はフックの法則の式になります。

塑性ひずみの発展方程式とひずみ空間内の硬化変数は以下で与えられます。

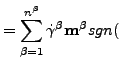$\displaystyle \mbox{\boldmath${\dot{\epsilon}^p}$}$ $\displaystyle = \sum_{\beta=1}^{n^\beta} \dot{\gamma}^\beta \mathbf{m^\beta} sgn($ $\displaystyle \mbox{\boldmath${\sigma}$}$ $\displaystyle : \mathbf{m^\beta} + q_2^\beta),$

(168)

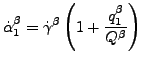$\displaystyle \dot{\alpha}_1^\beta = \dot{\gamma}^\beta \left (1 + \frac{q_1^\beta}{Q^\beta} \right)$

(169)

$\displaystyle \dot{\alpha}_2^\beta = \dot{\gamma}^\beta \left [\varphi^\beta sg... ...$} : \mathbf{m^\beta}+ q_2^\beta) + \frac{d^\beta q_2^\beta}{c^\beta} \right ].$

(170)

変数 $\dot{\gamma}^\beta$ は最適化理論[44] の Kuhn-Tucker 条件から求めた硬さ係数です。これは以下を満足するように求められます。

$\displaystyle \dot{\gamma}^\beta = \left\vert \dot{\epsilon}^{p^\beta} \right\vert,$

(171)

ここで $\dot{\epsilon}^{p^\beta}$ は向き β の流動率。塑性ひずみ率とそれぞれの向きの流動率は以下の式によって結びつけられます。

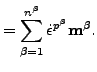$\displaystyle \mbox{\boldmath${\dot{\epsilon}^p}$}$ $\displaystyle = \sum_{\beta=1}^{n^\beta} \dot{\epsilon}^{p^\beta} \mathbf{m^\beta}.$

(172)

式（170）のパラメーター φ^β は以下のような累積せん断流動の絶対値です。

$\displaystyle \varphi^\beta=\phi^\beta+(1-\phi^\beta) e^{-\delta^\beta \int_0^t \dot{\gamma}^\beta dt}$

(173)

最後に、Cailletaud モデルではクリープ率は降伏超過のべき関数になります。

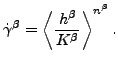$\displaystyle \dot{\gamma}^\beta = \left \langle \frac{h^\beta}{K^\beta} \right \rangle ^ {n^\beta}.$

(174)

ブラケット〈〉は負の値をゼロに、正の値をそのままにすることを意味します。つまり x < 0 では〈x〉 = 0 、x ≥ 0 では〈x〉 = x となります。

現在の umat ルーチンでは Nickel ベースの単結晶のために Cailletaud モデルが実装されています。すべり系は2つあります。4つのすべり面 {111} に、3つのすべり方向〈011〉がある8面体すべり系と、3つのすべり面 {001} に2つのすべり方向〈011〉を持つ立方体すべり系です。全ての8面体すべり方向、立方体すべり方向の定数は理論的なものです。さらにこの材料には3つの弾性定数があります。結果、各温度に対して21の定数を定義する必要があります。つまり弾性定数 C₁₁₁₁、C₁₁₂₂、C₁₂₁₂、さらに各すべり系ごとに $\{K^\beta,n^\beta,c^\beta,d^\beta,\phi^\beta,\delta^\beta,r_0^\beta,Q^\beta,b^\beta\}$ です。またこれらの定数とは別に18²の相互作用係数を定義する必要があります。これらは[49][50]に基づくもので、定数と見なされます。これらの値はルーチン内に含まれ、入力デッキでユーザーに影響を与えうることはありません。

材料定義は、材料名を定義する *MATERIAL から構成されます。この名前は必ず「SINGLE_CRYSTAL」から始まり、80文字以内でなければなりません。残りの66文字に関しては自由に設定することができます。材料定義内では *USER MATERIAL カードは以下を満たす必要があります。

完全な温度依存性を定義する必要がある場合はこの行を繰り返してください。

結晶の第1軸はグローバル座標系と一致するとみなされます。もしそうでない場合には *ORIENTATION カードを使用してローカル座標系を定義してください。

これらの変数は *EL PRINT キーワード（.datファイル）と *EL FILE キーワード（.frdファイル）で順番に従ってアクセスすることができます（SDVラベル）。また*DEPVAR カードを材料定義内で値60とともに設定する必要があります。

温度400に対して弾性定数 {135468., 68655., 201207.}、8面体パラメーター {1550., 3.89, 18.E4, 1500., 1.5, 100., 80., -80., 500.}、立方体パラメーター {980., 3.89, 9.E4, 1500., 2., 100., 70., -50.} の単結晶を定義。